UP Lambda-SKI cube

Type-Free Lambda Calculi (Lambdac)

The Type-Free Lambda Calculus

The type-free lambda calculus is a calculus employing a notation with just two primitive constructions, function application and functional abstraction. The semantics of the notation are determined by the process of substitution whereby the value of an argument to a function is substituted for occurrences of a place holder (known as a bound variable) in the body of the defining expression for the function, yielding an expression denoting the value of the function at the point denoted by the argument.

In this notation function application is written as juxtaposition, with the function on the left and the value to which it is applied on the right. No brackets are necessary unless the argument is an expression.

Functional abstraction is written using the special character "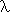lambda" as follows.

The function whose value at x can be obtained by evaluating the expression E x (in which occurrences of x are to be understood as placeholders for the value of the argument at which the value of the function is being determined) is written:

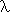lambdax.Ex

The character 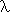lambda serves to introduce the abstraction, and the following variable is then a binding occurrence of that variable. Occurrences of that variable within the body of the abstraction are then bound to the binding occurrence (unless they fall inside the scope of another abstraction contained in the body of the first).

The pure lambda calculus was introduced by Church to study the solvability of problems in number theory. The widely accepted thesis that effective procedures over the natural numbers are just those which can be described in the pure lamdba calculus is known as "Church's Thesis".

The pure Lambda Calculus may be though of as an elaboration of Pure Combinatory Logic. It may be further modified either by introducing a simple type system, yielding a Pure Typed Lambda Calculus, or by introducing logical constants such as quantification, giving untyped or typed lambda logics.

up home © RBJ created 1995/12/9 modified 1999/6/1