|
An interpretation consists of a set of elements, which is called the domain of the interpretation, together with an assignment to each predicate letter of a set of finite sequences of elements from the domain.
A valuation is an assignment to each variable of an element in the domain of interpretation.
The truth value of a formula f under an interpretation i and valuation v is fpeval i v f, where fpeval is a (higher order) function taking three successive arguments, and is defined as follows (function application is shown as juxtaposition, brackets are not necessary for simple arguments):
| fpeval i v | (P x seqt) |  | (tseval v seqt)  (i x) (i x) |
| fpeval i v | ( f) f) |  |  (fpeval i v f) (fpeval i v f) |
| fpeval i v | (f1  f2) f2) |  | (fpeval i v f1)  (fpeval i v f2) (fpeval i v f2) |
| fpeval i v | ( x. f) x. f) |  |  y y  dom(i). fpeval i ( dom(i). fpeval i (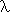 z. if z=x then y else v z) f z. if z=x then y else v z) f |
Where tseval evaluates a sequence of terms using a valuation v yielding a sequence of elements in the domain of interpretation, and may be defined:
| tseval v | nil | = | nil | |
| tseval v | ((Var x), seqt) | = | ((v x),(tseval v seqt)) |
|


 <formula>
<formula> <formula>
<formula> <letter>. <formula>
<letter>. <formula>
 (i x)
(i x)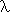 z. if z=x then y else v z) f
z. if z=x then y else v z) f A
A
 ©
©
 created 1997/10/18 modified 1997/10/25
created 1997/10/18 modified 1997/10/25