
The  Axes
Axes
Three three axes of the Lambda-SKI cube correspond to three independent ways in which pure combinatory logic can be extended.
Names associated with these axes provide a systematic naming convention for the eight types of logical system which are obtained by the various combinations of these extensions.
Variable Binding
Possibly the least significant extension from a theoretical standpoint is the addition of lambda abstraction, though this is very important for pragmatic reasons.
This extension permits a function to be defined using an expression for the value of the function in which occurrences of a chosen variable are used to mark places in the expression which are to be replaced when the function is evaluation by the value of the argument to the function.
An abstraction of this kind is written down using a lambda sign followed by the name of the variable which will be used for the argument, a full stop and then the expression for the function value.
e.g., the square function might be written as the lambda abstraction:
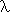 x. x*x
x. x*x
Types
A very signficant kind of extension is the addition of a type system.
A type system has advantages both for making the lambda calculus into a practical programming language and also for making it into a consistent logical system, though it is not essential for either of these purposes.
There are very many different types systems which may be used, of which the simplest is probably the one used by Church in his Simple Theory of Types [Church40].
Quantification
Pure combinatory logic is at bottom just an extremely simple programming language.
Adding lambda abstraction makes it no more expressive, adding a simple type system actually reduces what you can do with it!
If you want to use this as the basis for a logic, or for the foundations of mathematics, you need quantification (or something else which would permit quantifiers to be defined, e.g. equality).
The final axis of extension is the addition of some such constant, the effect of which is to transform a calculus (programming language) into a logic.
This must be done with some care, since the semantics of such extensions is tricky, and if you pick some logical rules without getting the semantics right you are likely to end up with an inconsistent logic, which is not a lot of use (though they do occasionally have some applications).
The simplest way to do this safely is again, Church's STT.
Church did the type system for the lambda calculus and added equality as a new primitive, obtaining an elegant higher order logic which is in widespread use to this day.
You don't need to have lambda abstraction to make a logic from combinatory logic using an equality primitive, but its easier that way, and you don't even need a type system, but that's even harder.

 ©
©
 created 1995/11/27 modified 1999/9/19
created 1995/11/27 modified 1999/9/19
 Axes
Axes

 Axes
Axes
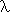 x. x*x
x. x*x
 ©
©
 created 1995/11/27 modified 1999/9/19
created 1995/11/27 modified 1999/9/19