

History and Philosophy
Mathematics is generally regarded as the exact subject par excellence.
But the language commonly used by mathematicians (in papers, monographs, and
even textbooks) can be remarkably vague; perhaps not when compared with
everyday speech but certainly when compared with the language used by
practitioners of other intellectual disciplines such as the natural sciences or
philosophy. [trybulec-z] point out that in a way this is natural: since
the underlying semantics of mathematics is generally clearer than that of other
disciplines, the mind is naturally trammelled into a precise mode of thinking,
and terminological exactness is less important. But a knowledgeable reader is
sometimes needed to separate rhetorical flourish from real content, and to
appreciate the context in which results are asserted. Some everyday phrases are
imbued with a particular significance; observe for example the crucial
distinction between a 'mapping into X' and a 'mapping onto X', or the
precise (albeit context-dependent) meaning of woolly-sounding expressions like
'for almost all x'. And on the other hand many issues that the author feels
are obvious or unimportant may be glossed over. [bourbaki-sets] stresses
the importance of ' abuses of language, without which any mathematical
text runs the risk of pedantry, not to say unreadability', but many of the
conventions go beyond mere abuse of language. Consider the following examples
taken from the early pages of [matsumura]:
- If f:A
 B is a ring homomorphism and J is an ideal of B, then
f-1(J) is an ideal of A and we denote this by A
B is a ring homomorphism and J is an ideal of B, then
f-1(J) is an ideal of A and we denote this by A  J; if A is a
subring of B and f is the inclusion map then this is the same as the usual
set-theoretic notion of intersection. In general this is not true, but
confusion does not arise.
J; if A is a
subring of B and f is the inclusion map then this is the same as the usual
set-theoretic notion of intersection. In general this is not true, but
confusion does not arise.
- When we say that R has characteristic p, or write char R = p, we
always mean that p > 0 is a prime number.
- In definitions and theorems about rings, it may sometimes happen that the
condition A
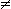 0 is omitted even when it is actually necessary.
0 is omitted even when it is actually necessary.
[trybulec-z] remark that the language of mathematical texts isn't
incontrovertibly a natural language at all; but it invariably contains a
substantial admixture of natural language, and that has all the usual potential
for ambiguity and imprecision. This might not be a problem if mathematics were
a small, unified subject easily graspable by a single practitioner. But on the
contrary mathematics is heading increasingly in the direction of
specialization, and it's not realistic to expect mathematical physicists, say,
to appreciate deeply all the theoretical results in topology, differential
geometry, numerical analysis and what not that they use.
There is also the question of the correctness of mathematical reasoning.
Mathematical proofs are subjected to peer review before publication, but there
are plenty of well-documented cases where published results turned out to be
faulty. A notable example is the purported proof of the 4-colour theorem by
[kempe]; the error in this proof was eventually pointed out in print by
[heaywood], and it is only with the work of [appel-4] that the
theorem has finally come to be accepted.1
The errors need not be deep mathematical ones, as shown by the following from
[littlewood-miscellany]:
Professor Offord and I recently committed ourselves to an odd mistake (Annals
of Mathematics (2) 49, 923, 1.5). In formulating a proof a plus sign got
omitted, becoming in effect a multiplication sign. The resulting false formula
got accepted as a basis for the ensuing fallacious argument. (In defence, the
final result was known to be true.)
A book by [lecat-errors] gave 130 pages of errors made by major
mathematicians up to 1900. With the abundance of theorems being published
today, often emanating from writers who are not trained mathematicians, one
fears that a project like Lecat's would be practically impossible, or at least
would demand a journal to itself!
We have separated the concerns of imprecision and incorrectness, but they are
linked. If one mathematician uses another's result without fully appreciating
the definitions underlying it or the conditions attached to it, this can lead
to errors. Moreover, as famously shown by [lakatos-pr], incorrectness and
imprecision can shade imperceptibly close to one another. Lakatos discusses how
Euler's theorem about polyhedra has changed over time. It was shown to be
incorrect, but rather than being overthrown, it merely evolved, incorporating
additional explicit conditions which formerly were either left unsaid or not
appreciated at all. In the final incarnation its validity stands almost as a
definition of a certain kind of polyhedron. This is not such an uncommon fate
for important theorems. For example, Stokes's theorem has been generalized so
much, and been associated with the development of so much technical machinery,
that the theorem itself is almost a triviality. Even if one does not subscribe
in full to Lakatos's thesis that mathematics has a strong empirical component
placing it almost on a par with physical sciences, such examples are worth
reflecting on.
The formalization of mathematics addresses both these questions, precision and
correctness. By formalization we mean expressing mathematics, both
statements and proofs, in a (usually small and simple) formal language with
strict rules of grammar and unambiguous semantics. The latter point bears
repeating: just writing something in a symbolic language is not sufficient for
formality if the semantics of that language is ill-defined.2 We can split the project of formalization into two parts:
- Formalizing the statements of theorems, and the implicit context
(definitions etc.) on which they depend.
- Formalizing the proofs of the results and subjecting them to precise
checking.
These are usually considered together, but perhaps merely stating theorems
formally without proving them has itself a valuable role. In the construction
of computer systems, formal specification has proved to be valuable in bringing
out unstated assumptions and clarifying thoughts --- it doesn't seem too
fanciful to suggest that there could be similar benefits for mathematics. In
practice, though, we are also interested in checking the correctness of proofs,
and formalization of the statements and then the proofs is a prerequisite for
doing this systematically.



 John Harrison
96/8/13; HTML by
John Harrison
96/8/13; HTML by  96/8/26
96/8/26
 B is a ring homomorphism and J is an ideal of B, then
f-1(J) is an ideal of A and we denote this by A
B is a ring homomorphism and J is an ideal of B, then
f-1(J) is an ideal of A and we denote this by A  J; if A is a
subring of B and f is the inclusion map then this is the same as the usual
set-theoretic notion of intersection. In general this is not true, but
confusion does not arise.
J; if A is a
subring of B and f is the inclusion map then this is the same as the usual
set-theoretic notion of intersection. In general this is not true, but
confusion does not arise.
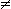 0 is omitted even when it is actually necessary.
0 is omitted even when it is actually necessary.



 John Harrison
96/8/13; HTML by
John Harrison
96/8/13; HTML by  96/8/26
96/8/26