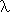[agerholm-dinf] Agerholm, S. (1994) Formalising a model of the {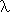}-calculus in {HOL-ST}.
Technical Report 354, University of Cambridge Computer Laboratory, New Museums Site, Pembroke Street, Cambridge, CB2 3QG, UK.

[aiello-meta] Aiello, L., Cecchi, C., and Sartini, D. (1986) Representation and use of metaknowledge.
Proceedings of the IEEE, 74, 1304--1321.

[allen-reflected] Allen, S., Constable, R., Howe, D., and Aitken, W. (1990) The semantics of reflected proof.
In Proceedings of the Fifth Annual Symposium on Logic in Computer Science, Los Alamitos, CA, USA, pp. 95--107. IEEE Computer Society Press.

[andrews-tps] Andrews, P. B., Bishop, M., Issar, S., Nesmith, D., Pfenning, F., and Xi, H. (1996) TPS: A theorem proving system for classical type theory.
Journal of Automated Reasoning, 16, 321--353.

[anonymous-qed] Anonymous (1994) The QED Manifesto.
In Bundy, A. (ed.), 12th International Conference on Automated Deduction, Volume 814 of Lecture Notes in Computer Science, Nancy, France, pp. 238--251. Springer-Verlag.

[appel-4] Appel, K. and Haken, W. (1976) Every planar map is four colorable.
Bulletin of the American Mathematical Society, 82, 711--712.

[anl-new-results] {Argonne National Laboratories} (1995) A summary of new results in mathematics obtained with Argonne's automated deduction software.
Unpublished; available on the Web as http://www.mcs.anl.gov/home/mccune/ar/new_results/.

[armando-building] Armando, A., Cimatti, A., and Viganò, L. (1993) Building and executing proof strategies in a formal metatheory.
In Torasso, P. (ed.), Advances in Artifical Intelligence: Proceedings of the Third Congress of the Italian Association for Artificial Intelligence, IA*AI'93, Volume 728 of Lecture Notes in Computer Science, Torino, Italy, pp. 11--22. Springer-Verlag.

[arnold-newtonhooke] Arnol'd, V. I. (1990) Huygens and Barrow, Newton and Hooke: pioneers in mathematical analysis and catastrophe theory from evolents to quasicrystals.
Birkhauser.
Translated from the Russian by Eric J.F. Primrose.

[arthan-undefinedness] Arthan, R. D. (1996) Undefinedness in Z: Issues for specification and proof.
In Kerber, M. (ed.), CADE-13 Workshop on Mechanization of Partial Functions.
Available on the Web as \verb+ftp://ftp.cs.bham.ac.uk/pub/authors/M.Kerber/96-CADE-WS/Arthan.ps.gz+ .

[beckert-posegga] Beckert, B. and Posegga, J. (1995) leanT ^AP: Lean, tableau-based deduction.
Journal of Automated Reasoning, 15, 339--358.
This is also available on the Web from http://i12www.ira.uka.de/ posegga/LeanTaP.ps.Z.

[benacerraf] Benacerraf, P. (1965) What numbers could not be.
Philosophical Review, 74, 47--73.
Reprinted in [benacerraf-putnam], pp. 272--294.

[benacerraf-putnam] Benacerraf, P. and Putnam, H. (1983) Philosophy of mathematics: selected readings (2nd ed.).
Cambridge University Press.

[biggs-graph] Biggs, N. L., Lloyd, E. K., and Wilson, R. J. (1976) Graph Theory 1736--1936.
Clarendon Press.

[bishop-bridges] Bishop, E. and Bridges, D. (1985) Constructive analysis, Volume 279 of Grundlehren der mathematischen Wissenschaften.
Springer-Verlag.

[blum-checking] Blum, M. (1993) Program result checking: A new approach to making programs more reliable.
In Lingas, A., Karlsson, R., and Carlsson, S. (eds.), Automata, Languages and Programming, 20th International Colloquium, ICALP93, Proceedings, Volume 700 of Lecture Notes in Computer Science, Lund, Sweden, pp. 1--14. Springer-Verlag.

[boole-article] Boole, G. (1848) The calculus of logic.
The Cambridge and Dublin Mathematical Journal, 3, 183--198.

[boulton-thesis] Boulton, R. J. (1993) Efficiency in a fully-expansive theorem prover.
Technical Report 337, University of Cambridge Computer Laboratory, New Museums Site, Pembroke Street, Cambridge, CB2 3QG, UK.
Author's PhD thesis.

[bourbaki-found] Bourbaki, N. (1948) Foundations of mathematics for the working mathematician.
Journal of Symbolic Logic, 14, 1--14.

[bourbaki-topology1] Bourbaki, N. (1966) General topology, Volume 1 of Elements of mathematics.
Addison-Wesley.
Translated from French {'Topologie Genérale'} in the series {'Eléments de mathématique'}, originally published by Hermann in 1966.

[bourbaki-sets] Bourbaki, N. (1968) Theory of sets.
Elements of mathematics. Addison-Wesley.
Translated from French {'Théorie des ensembles'} in the series {'Eléments de mathématique'}, originally published by Hermann in 1968.

[boyer-acl] Boyer, R. S. and Moore, J S. (1979) A Computational Logic.
ACM Monograph Series. Academic Press.

[boyer-moore-meta] Boyer, R. S. and Moore, J S. (1981) Metafunctions: proving them correct and using them efficiently as new proof procedures.
In Boyer, R. S. and Moore, J S. (eds.), The Correctness Problem in Computer Science, pp. 103--184. Academic Press.

[bridges-richmann] Bridges, D. and Richman, F. (1987) Varieties of Constructive Mathematics, Volume 97 of London Mathematical Society Lecture Note Series.
Cambridge University Press.

[debruijn-sad] de Bruijn, N. G. (1970) The mathematical language AUTOMATH, its usage and some of its extensions.
See [sadem], pp. 29--61.

[debruijn-Automat h] de Bruijn, N. G. (1980) A survey of the project AUTOMATH.
In Seldin, J. P. and Hindley, J. R. (eds.), To H. B. Curry: Essays in Combinatory Logic, Lambda Calculus, and Formalism, pp.\ 589--606. Academic Press.

[bryant] Bryant, R. E. (1986) Graph-based algorithms for Boolean function manipulation.
IEEE Transactions on Computers, C-35, 677--691.

[carnap-symlog] Carnap, R. (1958) Introduction to Symbolic Logic and its Applications.
Dover.
Translated by William H. Meyer and John Wilkinson; original German edition 'Einführing in die symbolische Logik' published by Julius Springer in 1954.

[church-number] Church, A. (1936) An unsolvable problem of elementary number-theory.
American Journal of Mathematics, 58, 345--363.

[church-types] Church, A. (1940) A formulation of the Simple Theory of Types.
Journal of Symbolic Logic, 5, 56--68.

[chwistek] Chwistek, L. (1922) Über die Antinomien de Principien der Mathematik.
Mathematische Annalen, 14, 236--243.

[clarke-zhao] Clarke, E. and Zhao, X. (1991) Analytica --- a theorem prover for Mathematica.
Technical report, School of Computer Science, Carnegie Mellon University.

[constable-programs] Constable, R. L., Knoblock, T. B., and Bates, J. L. (1985) Writing programs that construct proofs.
Journal of Automated Reasoning, 1, 285--326.

[corella-thesis] Corella, F. (1990) Mechanizing set theory.
Technical Report 232, University of Cambridge Computer Laboratory, New Museums Site, Pembroke Street, Cambridge, CB2 3QG, UK.
Author's PhD thesis.

[curzon-changes] Curzon, P. (1995) Tracking design changes with formal machine-checked proof.
The Computer Journal, 38, 91--100.

[davis-undecidable] Davis, M. (ed.) (1965) The Undecidable: Basic Papers on Undecidable Propositions, Unsolvable Problems and Computable Functions. Raven Press, NY.

[davis-schwartz] Davis, M. and Schwartz, J. T. (1979) Metatheoretic extensibility for theorem verifiers and proof-checkers.
Computers and Mathematics with Applications, 5, 217--230.

[dedekind-was] Dedekind, R. (1888) Was sind und was sollen die Zahlen?
Vieweg, Braunschweig.
English translation in [dedekind-essays].

[dedekind-essays] Dedekind, R. (ed.) (1901) Essays on the theory of numbers. Open Court, NY.
Reprinted by Dover, 1963.

[demillo-social] DeMillo, R., Lipton, R., and Perlis, A. (1979) Social processes and proofs of theorems and programs.
Communications of the ACM, 22, 271--280.

[dijkstra-invarianc e] Dijkstra, E. W. (1985) Invariance and non-determinacy.
In Hoare, C. A. R. and Shepherdson, J. C. (eds.), Mathematical Logic and Programming Languages, Prentice-Hall International Series in Computer Science, pp. 157--165. Prentice-Hall.
The papers in this volume were first published in the Philosophical Transactions of the Royal Society, Series A, vol. 312, 1984.

[farmer-imps] Farmer, W., Guttman, J., and Thayer, J. (1990) IMPS: an interactive mathematical proof system.
In Stickel, M. E. (ed.), 10th International Conference on Automated Deduction, Volume 449 of Lecture Notes in Computer Science, Kaiserslautern, Federal Republic of Germany, pp. 653--654. Springer-Verlag.

[feferman-transfini te] Feferman, S. (1962) Transfinite recursive progressions of axiomatic theories.
Journal of Symbolic Logic, 27, 259--316.

[fitch-book] Fitch, F. B. (1952) Symbolic Logic: an introduction.
The Ronald Press Company, New York.

[fowler] Fowler, H. W. (1965) A Dictionary of Modern English Usage (2nd, revised ed.).
Oxford University Press.
Revised by Sir Ernest Gowers.

[frege-beg] Frege, G. (1879) Begriffsschrift, eine der arithmetischen nachgebildete Formelsprache des reinen Denkens.
Louis Nebert, Halle.
English translation, 'Begriffsschrift, a formula language, modeled upon that of arithmetic, for pure thought' in [vanh], pp. 1--82.

[freyd-allegories] Freyd, P. J. and Scedrov, A. (1990) Categories, allegories.
North-Holland.

[vangasteren-shape] van Gasteren, A. J. M. (1990) On the shape of mathematical arguments, Volume 445 of Lecture Notes in Computer Science.
Springer-Verlag.
Foreword by E. W. Dijkstra.

[gentzen-investigatio ns] Gentzen, G. (1935) Untersuchungen über das logische Schliessen.
Mathematische Zeitschrift, 39, 176--210, 405--431.
This was Gentzen's Inaugural Dissertation at Göttingen. English translation, 'Investigations into Logical Deduction', in [gentzen], p. 68--131.

[gilmore-pm] Gilmore, P. C. (1960) A proof method for quantification theory: Its justification and realization.
IBM Journal of research and development, 4, 28--35.

[godel-undecidabl e] Gödel, K. (1931) Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme, I.
Monatshefte f{ür Mathematik und Physik}, 38, 173--198.
English translation, 'On Formally Undecidable Propositions of Principia Mathematica and Related Systems, I', in [vanh], pp. 592--618 or [davis-undecidable], pp. 4--38.

[godel-russell] Gödel, K. (1944) Russell's mathematical logic.
In The Philosophy of Bertrand Russell, Volume 5 of The Library of Living Philosophers, pp. 125--153. Northwestern University.
Reprinted in [benacerraf-putnam], pp. 447--469.

[gordon-st] Gordon, M. J. C. (1994) Merging HOL with set theory: preliminary experiments.
Technical Report 353, University of Cambridge Computer Laboratory, New Museums Site, Pembroke Street, Cambridge, CB2 3QG, UK.

[gordon-holbook] Gordon, M. J. C. and Melham, T. F. (1993) Introduction to {HOL: a theorem proving environment for higher order logic}.
Cambridge University Press.

[gordon-lcfbook] Gordon, M. J. C., Milner, R., and Wadsworth, C. P. (1979) Edinburgh {LCF: A Mechanised Logic of Computation}, Volume 78 of Lecture Notes in Computer Science.
Springer-Verlag.

[grothendieck-sga4] Grothendieck, A., Artin, M., and Verdier, J. L. (1972) Th{éorie des Topos et Cohomologie {\'E}tale des Schemas (SGA 4), vol. 1}, Volume 269 of Lecture Notes in Mathematics.
Springer-Verlag.

[grundy-fais] Grundy, J. (1996) A browsable format for proof presentation.
In Gefwert, C., Orponen, P., and Seppänen, J. (eds.), Proceedings of the Finnish Artificial Intelligence Society Symposium: Logic, Mathematics and the Computer, Volume 14 of Suomen Teko{älyseuran julkaisuja}, pp. 171--178. Finnish Artificial Intelligence Society.

[guard-sam] Guard, J. R., Oglesby, F. C., Bennett, J. H., and Settle, L. G. (1969) Semi-automated mathematics.
Journal of the ACM, 16, 49--62.

[halmos-ba] Halmos, P. R. (1963) Lectures on Boolean algebras, Volume 1 of Van Nostrand mathematical studies.
Van Nostrand.

[harrison-hol93] Harrison, J. (1993) A HOL decision procedure for elementary real algebra.
See [hol93], pp. 426--436.

[harrison-fmsd94] Harrison, J. (1994) Constructing the real numbers in HOL.
Formal Methods in System Design, 5, 35--59.

[harrison-cj95] Harrison, J. (1995) Binary decision diagrams as a HOL derived rule.
The Computer Journal, 38, 162--170.

[harrison-thery2] Harrison, J. and Théry, L. (1993) Extending the HOL theorem prover with a computer algebra system to reason about the reals.
See [hol93], pp. 174--184.

[heaywood] Heawood, P. J. (1890) Map-colour theorem.
Quarterly Journal of Pure and Applied Mathematics, 24, 332--338.
Reprinted in [biggs-graph].

[vanh] van Heijenoort, J. (ed.) (1967) From Frege to G{ödel: A Source Book in Mathematical Logic 1879--1931}. Harvard University Press.

[henkin-ptypes] Henkin, L. (1963) A theory of propositional types.
Fundamenta Mathematicae, 52, 323--344.

[hilbert-fgeom] Hilbert, D. (1899) Grundlagen der Geometrie.
Teubner.
English translation 'Foundations of Geometry' published in 1902 by Open Court, Chicago.

[hilbert-ackermann] Hilbert, D. and Ackermann, W. (1950) Principles of Mathematical Logic.
Chelsea.
Translation of 'Grundzüge der theoretischen Logik', 2nd edition (1938; first edition 1928); translated by Lewis M. Hammond, George G. Leckie and F. Steinhardt; edited with notes by Robert E. Luce.

[hobbes-leviathan] Hobbes, T. (1651) Leviathan.
Andrew Crooke.

[holmes-naive] Holmes, R. M. (1995) Naive set theory with a universal set.
Unpublished; available on the Web as http://math.idbsu.edu/faculty/holmes/naive1.ps.

[howe-computational] Howe, D. J. (1988) Computational metatheory in Nuprl.
In Lusk, E. and Overbeek, R. (eds.), 9th International Conference on Automated Deduction, Volume 310 of Lecture Notes in Computer Science, Argonne, Illinois, USA, pp. 238--257. Springer-Verlag.

[huet-saibi] Huet, G. and Saïbi, A. (1994) Constructive category theory.
Preprint, available on the Web as \verb+ftp://ftp.inria.fr/INRIA/Projects/coq/Gerard.Huet/Cat.dvi.Z+.

[jacobson1] Jacobson, N. (1989) Basic Algebra I (2nd ed.).
W. H. Freeman.

[hol93] Joyce, J. J. and Seger, C. (eds.) (1993) Proceedings of the 1993 International Workshop on the {HOL theorem proving system and its applications}, Volume 780 of Lecture Notes in Computer Science, UBC, Vancouver, Canada. Springer-Verlag.

[jutting-thesis] van Bentham Jutting, L. S. (1977) Checking Landau's ''Grundlagen'' in the {AUTOMATH System}.
Ph. D. thesis, Eindhoven University of Technology.
Useful summary in [nederpelt-automath], pp. 701--732.

[kelley] Kelley, J. L. (1975) General topology, Volume 27 of Graduate Texts in Mathematics.
Springer-Verlag.
First published by D. van Nostrand in 1955.

[kempe] Kempe, A. B. (1879) On the geographical problem of the four colours.
American Journal of Mathematics, 2, 193--200.
Reprinted in [biggs-graph].

[knoblock-constable] Knoblock, T. and Constable, R. (1986) Formalized metareasoning in type theory.
In Proceedings of the First Annual Symposium on Logic in Computer Science, Cambridge, MA, USA, pp. 237--248. IEEE Computer Society Press.

[knuth-bendix] Knuth, D. and Bendix, P. (1970) Simple word problems in universal algebras.
In Leech, J. (ed.), Computational Problems in Abstract Algebra. Pergamon Press.

[knuth-ss] Knuth, D. E. (1973) The Art of Computer Programming; Volume 3: Sorting and Searching.
Addison-Wesley Series in Computer Science and Information processing. Addison-Wesley.

[kreisel-hilbert] Kreisel, G. (1958) Hilbert's programme.
Dialectica, 12, 346--372.
Revised version in [benacerraf-putnam].

[kreisel-sad] Kreisel, G. (1970) Hilbert's programme and the search for automatic proof procedures.
See [sadem], pp. 128--146.

[kreisel-distractions] Kreisel, G. (1990) Logical aspects of computation: Contributions and distractions.
In Logic and Computer Science, Volume 31 of APIC Studies in Data Processing, pp. 205--278. Academic Press.

[kreisel-krivine] Kreisel, G. and Krivine, J.-L. (1971) Elements of mathematical logic: model theory (Revised second ed.).
Studies in Logic and the Foundations of Mathematics. North-Holland.
First edition 1967. Translation of the French 'Eléments de logique mathématique, théorie des modeles' published by Dunod, Paris in 1964.

[kumar-faust] Kumar, R., Kropf, T., and Schneider, K. (1991) Integrating a first-order automatic prover in the HOL environment.
In Archer, M., Joyce, J. J., Levitt, K. N., and Windley, P. J. (eds.), Proceedings of the 1991 International Workshop on the {HOL theorem proving system and its Applications}, University of California at Davis, Davis CA, USA, pp. 170--176. IEEE Computer Society Press.

[kunen] Kunen, K. (1980) Set Theory: An Introduction to Independence Proofs, Volume 102 of Studies in Logic and the Foundations of Mathematics.
North-Holland.

[lakatos-pr] Lakatos, I. (1976) Proofs and Refutations: the Logic of Mathematical Discovery.
Cambridge University Press.
Edited by John Worrall and Elie Zahar. Derived from Lakatos's Cambridge PhD thesis; an earlier version was published in the British Journal for the Philosophy of Science vol. 14.

[lakatos-proof] Lakatos, I. (1980) What does a mathematical proof prove?
In Worrall, J. and Currie, G. (eds.), Mathematics, science and epistemology. Imre Lakatos: Philosophical papers vol. 2, pp. 61--69. Cambridge University Press.

[lam-proof] Lam, C. W. H. (1990) How reliable is a computer-based proof?
The Mathematical Intelligencer, 12, 8--12.

[landau] Landau, E. (1930) Grundlagen der Analysis.
Leipzig.
English translation by F. Steinhardt: 'Foundations of analysis: the arithmetic of whole, rational, irrational, and complex numbers. A supplement to textbooks on the differential and integral calculus', published by Chelsea; 3rd edition 1966.

[lang-algebra] Lang, S. (1994) Algebra (3rd ed.).
Addison-Wesley.

[sadem] Laudet, M., Lacombe, D., Nolin, L., and Schützenberger, M. (eds.) (1970) Symposium on Automatic Demonstration, Volume 125 of Lecture Notes in Mathematics. Springer-Verlag.

[lecat-errors] Lecat, M. (1935) Erreurs de Mathématiciens.
Brussels.

[littlewood-mis cellany] Littlewood, J. E. (1986) Littlewood's Miscellany.
Cambridge University Press.
Edited by Bela Bollobas.

[lob-theorem] Löb, M. H. (1955) Solution of a problem of Leon Henkin.
Journal of Symbolic Logic, 20, 115--118.

[loveland-me1] Loveland, D. W. (1968) Mechanical theorem-proving by model elimination.
Journal of the ACM, 15, 236--251.

[maclane-mff] Mac Lane, S. (1986) Mathematics: Form and Function.
Springer-Verlag.

[mackenzie-proof] MacKenzie, D. (1995) The automation of proof: A historical and sociological exploration.
IEEE Annals of the History of Computing, 17(3), 7--29.

[marciszewski-murawski] Marciszewski, W. and Murawski, R. (1995) Mechanization of Reasoning in a Historical Perspective, Volume 43 of Pozna{\'n Studies in the Philosophy of the Sciences and the Humanities}.
Rodopi, Amsterdam.

[maslov-inverse] Maslov, S. J. (1964) An inverse method of establishing deducibility in classical predicate calculus.
Doklady Akademii Nauk, 159, 17--20.

[mathias-bourbaki] Mathias, A. R. D. (1991) The ignorance of Bourbaki.
Physis; rivista internazionale di storia della scienza (nuova serie), 28, 887--904.
Also in 'The Mathematical Intelligencer' vol. 14, nr. 3, pp. 4--13, 1992.

[matsumura] Matsumura, H. (1986) Commutative Ring Theory, Volume 8 of Cambridge Studies in Advanced Mathematics.
Cambridge University Press.
Translated from Japanese 'Kakan kan ron' by Miles Reid.

[matthews-fs0-theor y] Matthews, S. (1994) A theory and its metatheory in {FS₀}.
In Gabbay, D. (ed.), What is a Logic? Oxford University Press.

[megill-metamath] Megill, N. D. (1996) Metamath: A computer language for pure mathematics.
Unpublished; available on the Web from \verb+ftp://sparky.shore.net/members/ndm/metamath.tex.Z+.

[mehlhorn-checking] Mehlhorn, K. et al. (1996) Checking geometric programs or verification of geometric structures.
Unpublished; to appear in the proceedings of SCG'96. Available on the Web as http://www.mpi-sb.mpg.de/LEDA/articles/programc.dvi.Z.

[melham-tydef] Melham, T. F. (1989) Automating recursive type definitions in higher order logic.
In Birtwistle, G. and Subrahmanyam, P. A. (eds.), Current Trends in Hardware Verification and Automated Theorem Proving, pp. 341--386. Springer-Verlag.

[morse-sets] Morse, A. P. (1965) A theory of sets.
Academic Press.

[naur-pvf] Naur, P. (1994) Proof versus formalization.
BIT, 34, 148--164.

[nederpelt-automath] Nederpelt, R. P., Geuvers, J. H., and de Vrijer, R. C. (eds.) (1994) Selected Papers on Automath, Volume 133 of Studies in Logic and the Foundations of Mathematics. North-Holland.

[newell-simon] Newell, A. and Simon, H. A. (1956) The logic theory machine.
IRE Transactions on Information Theory, 2, 61--79.

[nidditch] Nidditch, P. H. (1957) Introductory formal logic of mathematics.
University Tutorial Press, London.

[paris-harrington] Paris, J. and Harrington, L. (1991) A mathematical incompleteness in Peano Arithmetic.
In Barwise, J. and Keisler, H. (eds.), Handbook of mathematical logic, Volume 90 of Studies in Logic and the Foundations of Mathematics, pp. 1133--1142. North-Holland.

[paulson-coalgebra] Paulson, L. C. (1994a) A concrete final coalgebra theorem for ZF set theory.
Technical Report 334, University of Cambridge Computer Laboratory, New Museums Site, Pembroke Street, Cambridge, CB2 3QG, UK.

[paulson-isabelleboo k] Paulson, L. C. (1994b) Isabelle: a generic theorem prover, Volume 828 of Lecture Notes in Computer Science.
Springer-Verlag.
With contributions by Tobias Nipkow.

[paulson-rubin] Paulson, L. C. and Gr\cabczewski, K. (1996) Mechanizing set theory: Cardinal arithmetic and the axiom of choice.
Journal of Automated Reasoning, to appear.
See also
http://www.cl.cam.ac.uk/Research/Reports/TR377-lcp-mechanising-set-theory.ps.gz.

[pollack-extensibilit y] Pollack, R. (1995) On extensibility of proof checkers.
In Dybjer, P., Nordström, B., and Smith, J. (eds.), Types for Proofs and Programs: selected papers from TYPES'94, Volume 996 of Lecture Notes in Computer Science, B\aastad, pp. 140--161. Springer-Verlag.

[pratt-prime] Pratt, V. (1975) Every prime has a succinct certificate.
SIAM Journal of Computing, 4, 214--220.

[prawitz-ipp] Prawitz, D. (1960) An improved proof procedure.
Theoria, 26, 102--139.

[prawitz-book] Prawitz, D. (1965) Natural deduction; a proof-theoretical study, Volume 3 of Stockholm Studies in Philosophy.
Almqvist and Wiksells.

[prawitz-pp] Prawitz, D., Prawitz, H., and Voghera, N. (1960) A mechanical proof procedure and its realization in an electronic computer.
Journal of the ACM, 7, 102--128.

[ramsey-fm] Ramsey, F. P. (1926) The foundations of mathematics.
Proceedings of the London Mathematical Society (2), 25, 338--384.

[rasiowa-sikorski] Rasiowa, H. and Sikorski, R. (1970) The Mathematics of Metamathematics (3rd ed.), Volume 41 of Monografie Matematyczne, Instytut Matematyczny Polskiej Akademii Nauk.
Polish Scientific Publishers.

[robinson-resolutio n] Robinson, J. A. (1965) A machine-oriented logic based on the resolution principle.
Journal of the ACM, 12, 23--41.

[rosser-ml] Rosser, J. B. (1953) Logic for Mathematicians.
McGraw-Hill.

[rubin-ac2] Rubin, H. and Rubin, J. E. (1985) Equivalents of the axiom of choice, {II}, Volume 116 of Studies in Logic and the Foundations of Mathematics.
North-Holland.
First edition in the same series, 1963.

[rudnicki-obvious] Rudnicki, P. (1987) Obvious inferences.
Journal of Automated Reasoning, 3, 383--393.

[russell-autobiog] Russell, B. (1968) The autobiography of Bertrand Russell.
Allen & Unwin.

[shostak-presburger] Shostak, R. (1979) A practical decision procedure for arithmetic with function symbols.
Journal of the ACM, 26, 351--360.

[slind-thesis] Slind, K. (1991) An implementation of higher order logic.
Technical Report 91-419-03, University of Calgary Computer Science Department, 2500 University Drive N. W., Calgary, Alberta, Canada, TN2 1N4.
Author's Masters thesis.

[spivey-understanding] Spivey, J. M. (1988) Understanding Z: a specification language and its formal semantics, Volume 3 of Cambridge Tracts in Theoretical Computer Science.
Cambridge University Press.

[stalmarc k-patent] St\aalmarck, G. (1994) System for determining propositional logic theorems by applying values and rules to triplets that are generated from Boolean formula.
United States Patent number 5,276,897; see also Swedish Patent 467 076.

[stickel-pttp] Stickel, M. E. (1988) A Prolog Technology Theorem Prover: Implementation by an extended Prolog compiler.
Journal of Automated Reasoning, 4, 353--380.

[gentzen] Szabo, M. E. (ed.) (1969) The collected papers of Gerhard Gentzen, Studies in Logic and the Foundations of Mathematics. North-Holland.

[szczerba-mizar] Szczerba, L. W. (1989) The use of Mizar MSE in a course in foundations of geometry.
In Srzednicki, J. (ed.), Initiatives in logic, Volume 2 of Reason and argument series. M. Nijhoff.

[takeuti-uses] Takeuti, G. (1978) Two applications of logic to mathematics.
Number 13 in Publications of the Mathematical Society of Japan. Iwanami Shoten, Tokyo.
Number 3 in Kanô memorial lectures.

[tarski-truth] Tarski, A. (1936) Der Wahrheitsbegriff in den formalisierten Sprachen.
Studia Philosophica, 1, 261--405.
English translation, 'The Concept of Truth in Formalized Languages', in [tarski-lsm], pp. 152--278.

[tarski-grothendieck] Tarski, A. (1938) Über unerreichbare Kardinalzahlen.
Fundamenta Mathematicae, 30, 176--183.

[tarski-decision] Tarski, A. (1951) A Decision Method for Elementary Algebra and Geometry.
University of California Press.
Previous version published as a technical report by the RAND Corporation, 1948; prepared for publication by J. C. C. McKinsey.

[tarski-lsm] Tarski, A. (ed.) (1956) Logic, Semantics and Metamathematics. Clarendon Press.

[troelstra-con1] Troelstra, A. S. and van Dalen, D. (1988) Constructivism in mathematics, vol. 1, Volume 121 of Studies in Logic and the Foundations of Mathematics.
North-Holland.

[trybulec-allc] Trybulec, A. (1978) The Mizar-QC/6000 logic information language.
ALLC Bulletin (Association for Literary and Linguistic Computing), 6, 136--140.

[trybulec-z] Trybulec, Z. and Swi\ceczkowska, H. (1991-1992) The language of mathematical texts.
Studies in Logic, Grammar and Rhetoric, 10/11, 103--124.

[turing] Turing, A. M. (1936) On computable numbers, with an application to the Entscheidungsproblem.
Proceedings of the London Mathematical Society (2), 42, 230--265.

[turing-ordinals] Turing, A. M. (1939) Systems of logic based on ordinals.
Proceedings of the London Mathematical Society (2), 45, 161--228.
Reprinted in [davis-undecidable], pp. 154--222.

[upsenskii-mechan ics] Upsenskii, V. A. (1961) Some Applications of Mechanics to Mathematics, Volume 3 of Popular lectures in mathematics.
Pergamon.
Translated from the Russian by Halina Moss; translation editor Ian N. Sneddon.

[wadler-blott] Wadler, P. and Blott, S. (1989) How to make ad-hoc polymorphism less ad hoc.
In Conference record of the 16th annual {ACM symposium on principles of programming languages (POPL)}, Association for Computing Machinery.

[wang-mm] Wang, H. (1960) Toward mechanical mathematics.
IBM Journal of research and development, 4, 2--22.

[whitehead-intro] Whitehead, A. N. (1919) An Introduction to Mathematics.
Williams and Norgate.

[whitehead-principia] Whitehead, A. N. and Russell, B. (1910) Principia Mathematica (3 vols).
Cambridge University Press.

[wiener-pair] Wiener, N. (1914) A simplification of the logic of relations.
Proceedings of the Cambridge Philosophical Society, 17, 387--390.

[yamamoto-graphs] Yamamoto, M., Nishizaha, S.-y., Hagiya, M., and Toda, Y. (1995) Formalization of planar graphs.
In Windley, P. J., Schubert, T., and Alves-Foss, J. (eds.), Higher Order Logic Theorem Proving and Its Applications: Proceedings of the 8th International Workshop, Volume 971 of Lecture Notes in Computer Science, Aspen Grove, Utah, pp. 369--384. Springer-Verlag.

[zermelo-new] Zermelo, E. (1908) Neuer Beweis für die Möglichkeit einer wohlordnung.
Mathematische Annalen, 65, 107--128.
English translation, 'A new proof of the possibility of a wellordering' in [vanh], pp. 183--198.

John Harrison 96/8/13; HTML by 96/8/16