

Formalizing mathematics
In formalizing mathematics, we must rephrase informal constructs in terms of
formal ones, which is merely an extreme case of defining non-rigorous concepts
rigorously. This isn't always easy, but there can be surprising successes ---
for example, before Turing it would have seemed implausible that a simple and
rigorous definition of 'computable' could be given. For a good historical
precedent, consider how Bolzano and Weierstrass arrived at rigorous
' -
-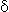 ' definitions of notions like limits and continuity. We may
have our own intuitive ideas of what a continuous function is: perhaps one
whose graph we can draw without taking our pencil from the graph paper, or
which passes through all intermediate values. But the definition of continuity
which is now standard is neither of these; we say a function f:R
' definitions of notions like limits and continuity. We may
have our own intuitive ideas of what a continuous function is: perhaps one
whose graph we can draw without taking our pencil from the graph paper, or
which passes through all intermediate values. But the definition of continuity
which is now standard is neither of these; we say a function f:R  R is continuous on R iff:
R is continuous on R iff:
 x
x  R.
R. 
 > 0.
> 0. 
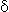 > 0.
> 0.  x'.
|x - x'| <
x'.
|x - x'| < 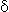
 |f(x) - f(x')| <
|f(x) - f(x')| < 
In what sense is this or any other formal definition 'right'? Why not take the
intermediate value property (called 'Darboux continuity') instead?
 x, x', z
x, x', z  R.
x < x'
R.
x < x'  (f(x) < z < f(x')
(f(x) < z < f(x')  f(x') < z < f(x))
f(x') < z < f(x))

 w. x < w < x'
w. x < w < x'  f(w) = z
f(w) = z
Such worries can be allayed when the various plausible-looking formalizations
are all provably equivalent. For example, the various definitions of
computability in terms of Turing machines, Markov algorithms, general recursive
functions, untyped 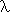 -calculus, production systems and so forth all
turned out so. But here this is not the case: continuity implies Darboux
continuity but not conversely.26 The usual definition of continuity
has probably won out because it is intuitively the most satisfying, leads to
the tidiest theory or admits the most attractive generalization to other metric
and topological structures. But note that it also led to the counterintuitive
pathologies of real analysis which, as we have already remarked, caused such
disquiet once. This example well illustrates how formalization can be a
difficult and creative task, and that the formal version of a concept can take
on an unexpected life of its own. However, since present-day mathematics is
mostly quite rigorous, the final step to complete formalization shouldn't
usually be so problematical.
-calculus, production systems and so forth all
turned out so. But here this is not the case: continuity implies Darboux
continuity but not conversely.26 The usual definition of continuity
has probably won out because it is intuitively the most satisfying, leads to
the tidiest theory or admits the most attractive generalization to other metric
and topological structures. But note that it also led to the counterintuitive
pathologies of real analysis which, as we have already remarked, caused such
disquiet once. This example well illustrates how formalization can be a
difficult and creative task, and that the formal version of a concept can take
on an unexpected life of its own. However, since present-day mathematics is
mostly quite rigorous, the final step to complete formalization shouldn't
usually be so problematical.



 John Harrison
96/8/13; HTML by
John Harrison
96/8/13; HTML by  96/8/16
96/8/16
 -
-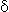 ' definitions of notions like limits and continuity. We may
have our own intuitive ideas of what a continuous function is: perhaps one
whose graph we can draw without taking our pencil from the graph paper, or
which passes through all intermediate values. But the definition of continuity
which is now standard is neither of these; we say a function f:R
' definitions of notions like limits and continuity. We may
have our own intuitive ideas of what a continuous function is: perhaps one
whose graph we can draw without taking our pencil from the graph paper, or
which passes through all intermediate values. But the definition of continuity
which is now standard is neither of these; we say a function f:R  R is continuous on R iff:
R is continuous on R iff:


 x
x 
 |f(x) - f(x')| <
|f(x) - f(x')| <  (f(x) < z < f(x')
(f(x) < z < f(x')  f(x') < z < f(x))
f(x') < z < f(x)) 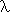 -calculus, production systems and so forth all
turned out so. But here this is not the case: continuity implies Darboux
continuity but not conversely.
-calculus, production systems and so forth all
turned out so. But here this is not the case: continuity implies Darboux
continuity but not conversely.
 John Harrison
96/8/13; HTML by
John Harrison
96/8/13; HTML by  96/8/16
96/8/16