

Formalization
There is no reason to be dogmatic about what is the 'natural' formalization of
informal (or preformal) notions. We do not claim that reductionism always
reflects the most interesting aspects of mathematics --- in fact as Mac Lane
has remarked, it can give a rather one-sided view of mathematical activity ---
but this is no more a problem than the fact that formal grammar rules do not
contribute to poetry. And we should certainly avoid regarding the
implementability of mathematical concepts as sets, say, as constituting some
kind of ontological discovery --- this view is rightly parodied by
[benacerraf]. Rather, it's an interesting and surprising practical
discovery about the flexibility of set theory, to be compared with Gentzen's
discoveries about the flexibility of a simple inferential apparatus. (At the
same time the reduction is not without philosophical significance: in
particular the consistency of practically all of mathematics can be reduced to
the problem of whether ZF set theory is consistent, so our foundational
concerns tend to come home to roost in set theory.)
With these disclaimers in mind, let's look now at a few examples of how the
basic concepts of formal systems can be used to define other notions. We'll
arrange these in order of the amount of light they throw on the informal
concept (in our opinion).
- Kuratowski showed that ordered pairs could be defined by (x,y) =
{x,{x,y}} (a more complicated alternative was earlier proposed by
[wiener-pair]). However it seems that this tells us nothing new about
ordered pairs, except for pathological theorems which we don't want anyway.
Indeed in stratified set theories like Quine's NFU [holmes-naive] and work
in coinductive definitions [paulson-coalgebra], another definition is
normally used.
- von Neumann's definition of the ordinals is often used to identify the
natural numbers with the set \omega of finite ordinals. This means that 0 =
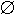 , 1 = {0}, 2 = {0, 1} etc. Although this is also quite arcane
and ad hoc (do we really want 0
, 1 = {0}, 2 = {0, 1} etc. Although this is also quite arcane
and ad hoc (do we really want 0  1?) it does have the benefit of
streamlining and simplifying a lot of theorems about natural numbers and
integrating them with their counterparts for ordinals and cardinals. Indeed
[halmos-ba] finds the use of 2 as a canonical 2-element set
sufficiently convenient to remark on it.
1?) it does have the benefit of
streamlining and simplifying a lot of theorems about natural numbers and
integrating them with their counterparts for ordinals and cardinals. Indeed
[halmos-ba] finds the use of 2 as a canonical 2-element set
sufficiently convenient to remark on it.
- We identify sequences indexed by the natural numbers, as used for example
in real analysis, with functions out of N. It's quite conceivable that one
could work with sequences without making explicitly the realization that the
two concepts are identical. However it seems there are no reasons for forcing a
distinction, so here the formalization is a unifying and simplifying force. In
fact, this observation seems first to have appeared with Peano's '
Formulaire', so it provides a concrete example of a mathematical development
being stimulated by a programme of formalization.
- Variable binding constructs (extensional ones anyway), such as summation,
integration and differentiation, can all be regarded as a higher order operator
applied to a lambda-term. That is,
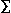 i=110 i is 'really'
SUM(1,10,
i=110 i is 'really'
SUM(1,10,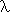 i. i) while the derivative notation d/(dx) x2 is
really DIFF(x,
i. i) while the derivative notation d/(dx) x2 is
really DIFF(x,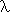 x. x2). This really can be valuable, confronting us with
awkward constructs where the everyday notation confuses free and bound
variables or a function with its value. For example, in the example above of
Leibniz notation for differentiation, x has both free and bound occurrences.
(It's precisely analogous to
x. x2). This really can be valuable, confronting us with
awkward constructs where the everyday notation confuses free and bound
variables or a function with its value. For example, in the example above of
Leibniz notation for differentiation, x has both free and bound occurrences.
(It's precisely analogous to 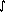 0x 2 x dx, except that here the
standard notation separates the two instances.) The breakdown to a lambda-term
has helped to make this explicit. Though the Leibniz notation is familiar, it
can be awkward and is often abandoned in advanced or multivariate work. Other
notations like f'(x) seem better, but can still lead to confusion; the author
has witnessed a heated debate on sci.math among good mathematicians over
whether f'(g(x)) denotes the derivative of f evaluated at g(x) (this view
seems most popular) or the derivative of f o g evaluated at x ('the
prime notation (f') is a shorthand notation for [the] derivative of a
univariate function with respect to the free variable.')
0x 2 x dx, except that here the
standard notation separates the two instances.) The breakdown to a lambda-term
has helped to make this explicit. Though the Leibniz notation is familiar, it
can be awkward and is often abandoned in advanced or multivariate work. Other
notations like f'(x) seem better, but can still lead to confusion; the author
has witnessed a heated debate on sci.math among good mathematicians over
whether f'(g(x)) denotes the derivative of f evaluated at g(x) (this view
seems most popular) or the derivative of f o g evaluated at x ('the
prime notation (f') is a shorthand notation for [the] derivative of a
univariate function with respect to the free variable.')



 John Harrison
96/8/13; HTML by
John Harrison
96/8/13; HTML by  96/8/16
96/8/16
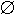 , 1 = {0}, 2 = {0, 1} etc. Although this is also quite arcane
and ad hoc (do we really want 0
, 1 = {0}, 2 = {0, 1} etc. Although this is also quite arcane
and ad hoc (do we really want 0  1?) it does have the benefit of
streamlining and simplifying a lot of theorems about natural numbers and
integrating them with their counterparts for ordinals and cardinals. Indeed
[halmos-ba] finds the use of 2 as a canonical 2-element set
sufficiently convenient to remark on it.
1?) it does have the benefit of
streamlining and simplifying a lot of theorems about natural numbers and
integrating them with their counterparts for ordinals and cardinals. Indeed
[halmos-ba] finds the use of 2 as a canonical 2-element set
sufficiently convenient to remark on it.
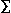 i=110 i is 'really'
SUM(1,10,
i=110 i is 'really'
SUM(1,10,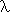 i. i) while the derivative notation d/(dx) x2 is
really DIFF(x,
i. i) while the derivative notation d/(dx) x2 is
really DIFF(x,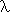 x. x2). This really can be valuable, confronting us with
awkward constructs where the everyday notation confuses free and bound
variables or a function with its value. For example, in the example above of
Leibniz notation for differentiation, x has both free and bound occurrences.
(It's precisely analogous to
x. x2). This really can be valuable, confronting us with
awkward constructs where the everyday notation confuses free and bound
variables or a function with its value. For example, in the example above of
Leibniz notation for differentiation, x has both free and bound occurrences.
(It's precisely analogous to 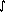 0x 2 x dx, except that here the
standard notation separates the two instances.) The breakdown to a lambda-term
has helped to make this explicit. Though the Leibniz notation is familiar, it
can be awkward and is often abandoned in advanced or multivariate work. Other
notations like f'(x) seem better, but can still lead to confusion; the author
has witnessed a heated debate on sci.math among good mathematicians over
whether f'(g(x)) denotes the derivative of f evaluated at g(x) (this view
seems most popular) or the derivative of f o g evaluated at x ('the
prime notation (f') is a shorthand notation for [the] derivative of a
univariate function with respect to the free variable.')
0x 2 x dx, except that here the
standard notation separates the two instances.) The breakdown to a lambda-term
has helped to make this explicit. Though the Leibniz notation is familiar, it
can be awkward and is often abandoned in advanced or multivariate work. Other
notations like f'(x) seem better, but can still lead to confusion; the author
has witnessed a heated debate on sci.math among good mathematicians over
whether f'(g(x)) denotes the derivative of f evaluated at g(x) (this view
seems most popular) or the derivative of f o g evaluated at x ('the
prime notation (f') is a shorthand notation for [the] derivative of a
univariate function with respect to the free variable.')



 John Harrison
96/8/13; HTML by
John Harrison
96/8/13; HTML by  96/8/16
96/8/16