

Feasibility
We have stated that the computer can handle tedious low-level details of proof.
This isn't just an airy idea; on the contrary the LCF methodology allows the
user to create higher-level proof structures which decompose to simple
primitives inside the computer. But what grounds do we have for believing that
this is practical even for a computer? (Accepting that some kind of
definitional principle will be used as detailed above.) It's well-known that
computers are amazingly fast, and getting faster, but it's equally well-known
that their speed cannot defeat problems that have an inherent combinatorial
explosion. The fact that fully automatic theorem provers have not
displaced human mathematicians, and that the World Chess Champion is not (quite
yet) a computer, are evidence of this. For example, if the length of a fully
formal proof were an exponential function of the length of an informal proof,
then the proposed approach would probably be doomed.
We've already seen that for any formal system of the kind we need to consider,
there are true statements which aren't provable in the system (Gödel's first
theorem). At the same time we have argued that such statements are pathologies
and we're unlikely to hit them in practice. We will make an exactly parallel
claim about the feasibility, rather than possibility in principle,
of proofs.
The measure of feasibility will be the size of a proof, which is meant to
denote something like the number of symbols in the proof based on a finite
alphabet --- this seems the most reasonable practical measure. Certainly, from
a theoretical perspective, there must be sentences out there whose proofs are
possible but not feasible. Indeed, given any (total) recursive function f
(e.g. a large constant function or a huge tower of exponentials), there are
provable sentences of size n that have no proofs of size 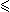 f(n). For
otherwise, provability would be decidable (just check all possible proofs up to
size f(n)), contradicting the results of Church and Turing that the
Entscheidungsproblem is unsolvable. More explicitly, we can modify Gödel's
diagonal argument and exhibit a sentence which says not 'I am unprovable', but
rather 'all proofs of me are unacceptably big':39
f(n). For
otherwise, provability would be decidable (just check all possible proofs up to
size f(n)), contradicting the results of Church and Turing that the
Entscheidungsproblem is unsolvable. More explicitly, we can modify Gödel's
diagonal argument and exhibit a sentence which says not 'I am unprovable', but
rather 'all proofs of me are unacceptably big':39



 p. Prov(p,
p. Prov(p,

 )
)  size(p) > f(
size(p) > f(

 )
)
Now, whether or not there are proofs of  whose size is bounded by
f(
whose size is bounded by
f(

 ) is decidable, and so
) is decidable, and so  is provable iff it is true. But
is provable iff it is true. But
 cannot be false, since that would mean there exists a proof of it,
indeed, one within the stated size bounds. Therefore
cannot be false, since that would mean there exists a proof of it,
indeed, one within the stated size bounds. Therefore  must be true,
provable, and yet have no proof within the stated bounds.
must be true,
provable, and yet have no proof within the stated bounds.
But now we claim once again that all such theorems are likely to be theoretical
pathologies, never to arise in 'normal' mathematics. Of course such a claim is
rather bold, and always open to refutation, but we can at least point to some
agreeable empirical evidence. First, looking at a modern, rigorous mathematical
textbook such as Bourbaki's, it's hard to see how an unbridgeable gap between
informal and formal proofs could arise. And in practice some significant pieces
of mathematics have been formalized, e.g. in Mizar, without any exponential
dependency appearing. On the contrary, there is some empirical evidence so far
that the length of a formal proof is a fairly modest linear function of
the length of a thorough textbook proof, as explicitly stated by
[debruijn-sad]:
A very important thing that can be concluded from all writing experiments is
the constancy of the loss factor. The loss factor expresses what we lose
in shortness when translating very meticulous 'ordinary' mathematics into
AUTOMATH. This factor may be very big, something like 10 or 20 (or 50), but it
is constant; it does not increase if we go further in the book. It would not be
too hard to push the constant factor down by efficient abbreviations.
Of course, the 'very meticulous' should be noted; Landau's book is a most
unusual one, and de Bruijn chose it after great deliberation. Although Mizar
has been used for an unrivalled number of mathematical formalizations, we are
unaware of any published comparisons between the original textual sources (such
as they are) and the resulting formal texts. Perhaps this is because the Mizar
formalizations are usually arrived at independently after consulting many
sources, rather than by translating existing texts or papers directly. However,
more efforts of this latter kind should throw new light on the question we are
considering. One attempt to follow a textbook faithfully is detailed by
[paulson-rubin]. They translated the early parts of set theory books by
[kunen] and [rubin-ac2] into Isabelle, and found that
the relationship between the size of the formal and informal texts was much
more variable. (Though not to the extent of infeasibility, it should be
stressed. They merely had to work rather harder themselves at certain points.)



 John Harrison
96/8/13; HTML by
John Harrison
96/8/13; HTML by  96/8/16
96/8/16
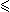 f(n). For
otherwise, provability would be decidable (just check all possible proofs up to
size f(n)), contradicting the results of Church and Turing that the
Entscheidungsproblem is unsolvable. More explicitly, we can modify Gödel's
diagonal argument and exhibit a sentence which says not 'I am unprovable', but
rather 'all proofs of me are unacceptably big':39
f(n). For
otherwise, provability would be decidable (just check all possible proofs up to
size f(n)), contradicting the results of Church and Turing that the
Entscheidungsproblem is unsolvable. More explicitly, we can modify Gödel's
diagonal argument and exhibit a sentence which says not 'I am unprovable', but
rather 'all proofs of me are unacceptably big':39





 p. Prov(p,
p. Prov(p,
 )
)  size(p) > f(
size(p) > f(
 John Harrison
96/8/13; HTML by
John Harrison
96/8/13; HTML by  96/8/16
96/8/16