  p. Prov(p, p. Prov(p,   ) )
 
|


If our speculation above is wrong, what is to be done when we come across an inference pattern that can't be implemented efficiently as an LCF derived rule? One alternative is to throw in whatever additional proof procedures might be deemed necessary. But for a serious project of formalization, we need a high level of assurance that the rule is correct. If it doesn't actually perform a formal proof, how can this be done?
One idea is to use metatheory. Suppose we formalize the object logic under consideration, its syntax and its notion of provability, in an additional layer of logic, the metalogic. The idea is that metatheorems (i.e. theorems in the metalogic) can then be proved which justify formally the possibility of proving a result in the object logic, without actually producing the proof in complete detail. One can use another layer of logic for this purpose, as discussed by [pollack-extensibility]. This metalogic can then be particularly simple and transparent, since few mathematical resources are needed to support the proofs of typical metatheorems. However, it's also possible to use the same logic; this is often referred to as reflection. From Gödel's work we already know how a system can formalize its own notion of provability. The only extra ingredient needed is a rule acting as a bridge between the internal formalization and the logic itself:44
  p. Prov(p, p. Prov(p,   ) )
 
|
It is clear that if the system is 1-consistent, this rule does not introduce
any new theorems, since all provable existential statements are true. However
the absence of hypotheses in the above theorems was crucial. The subtly
different rule with a nonempty set of hypotheses, or equivalently an additional
axiom scheme of the form  (
( p. Prov(p,
p. Prov(p,

 ))
)) 
 does make the logic stronger. In the special case where
does make the logic stronger. In the special case where  is F, it
amounts to a statement of consistency, which Gödel's second theorem rules
out, and in fact [lob-theorem] proved that such a theorem is provable in
the original system only in the trivial case where
is F, it
amounts to a statement of consistency, which Gödel's second theorem rules
out, and in fact [lob-theorem] proved that such a theorem is provable in
the original system only in the trivial case where 
 . Since these
assertions amount to an expression of confidence in the formal system, as seen
by reflecting on it from outside (the system is consistent, everything provable
is true),45 they
were dubbed 'reflection principles' by [feferman-transfinite], who,
following on from work by [turing-ordinals], investigated their iterated
addition as a principled way of making a formal system stronger. Our reflection
rules are intended rather to be a principled way of making proofs in a system
easier.
. Since these
assertions amount to an expression of confidence in the formal system, as seen
by reflecting on it from outside (the system is consistent, everything provable
is true),45 they
were dubbed 'reflection principles' by [feferman-transfinite], who,
following on from work by [turing-ordinals], investigated their iterated
addition as a principled way of making a formal system stronger. Our reflection
rules are intended rather to be a principled way of making proofs in a system
easier.
The value of using metalogic or reflection in this way depends, of course, on the fact that the metalogical proof of provability is easier (in some practically meaningful sense) than doing a full proof in the object logic.46 For example, this definitely seems to be the case for the Deduction Theorem and Skolemization steps discussed above: the metatheorem can be established once and for all in a general form by induction over the structure of object logic proofs, and thereafter instantiated for the cases in hand very cheaply. But we've already expressed scepticism over whether these examples are realistic for logics that one would actually use in practice.
The most popular examples cited are simple algebraic manipulations. Suppose one wants to justify a1 + ... + an = b1 + ... + bn (for real numbers, say) where the ai and bi are permutations of each other. An object-level proof would need to rewrite delicately with the associative and commutative laws; this is in fact what HOL's function AC_CONV does automatically. When implemented in a simple-minded way this takes O(n2) time; even when done carefully, O(n log(n)). However we can prove a metatheorem stating that if the multisets {a1, ..., an} and {b1, ..., bn} are equal, then the equation holds, without any further proof. [davis-schwartz] say confidently that 'the introduction of an appropriate ''algebra'' rule of inference shortens to 1 the difficulty of a sentence which asserts an algebraic identity'. But assigning a difficulty of 1 is of no practical significance. What of the complexity of checking multiset equality? In fact, it is O(n2) in the worst case, according to [knuth-ss]. Even if the elements are pairwise orderable somehow, we can't do better than O(n log(n)). So all this additional layer of complexity, and the tedium of proving a precise metatheorem, has achieved nothing except perhaps shaving something off the constant factor.
The constant factor is not even likely to change much. However it would change a lot more if the multiset equality test didn't have to be performed in some formal system, but could be evaluated directly by a program. This suggests another popular variant of the reflection idea: computational reflection. The idea is to verify that a program will correctly implement a rule of inference (e.g. correctly test for multiset equality and in the case of success, add the appropriate equation to the stock of theorems), then add that program to the implementation of the theorem prover, so thereafter it can be executed directly. This does indeed offer much more efficiency, and in certain special situations like arithmetical calculation, the speedup could be considerable. It would also be a systematic way of gaining confidence in the many theorems which are nowadays proved with the aid of computer checking. The proof of the 4-colour theorem has already been mentioned; more prosaic examples include simply assertions that large numbers are prime. Journals in some fields already have to confront difficult questions about what constitutes a proof in this context; the issue is discussed by [lam-proof] for example.
However there are a number of difficulties with the scheme. In particular, correctly formalizing the semantics of real programming languages, and then proving nontrivial programs correct, is difficult. The formal system becomes dramatically more complicated, since its rules effectively include the full semantics of the implementation language, instead of being separate and abstract. (This has a negative effect on the possibility of checking proofs using simple proof-checking programs, an oft-suggested idea to increase confidence in the correctness of machine-checked proofs.) And finally, reflection, though extensively studied, has not often been exploited in practice, the work of [boyer-moore-meta] being probably the most significant example to date.47
We should add that the idea of proving program correctness doesn't necessarily demand some kind of logical reflection principle to support it. Boyer and Moore, for example, need no such thing. Typical decision procedures only involve a rather restricted part of the logic (e.g. tautologies or arithmetic inequalities), and the semantics of this fragment can perfectly easily be internalized, even though by Tarski's theorem this cannot be done for the whole logic. (Nuprl's type theory, stratified by universe level, allows one to come very close to the ideal: the semantics of one layer can be formalized in the next layer up.) Ostensibly 'syntactic' manipulations can often be done directly in ordinary logic or set theory, defining some appropriate semantics; following [howe-computational], this is often called 'partial reflection'. For example, the above method for justifying an AC rearrangement based on multiset equality can easily be carried out in the object theory.
We should also point out the following. It is often stated that, issues of efficiency apart, some of the theorems in mathematics books are metatheorems, or can only be proved using metatheory --- 'most of' them according to [aiello-meta]. [matthews-fs0-theory] is one of the few who cites an example:
For instance in a book on algebra one might read:'If A is an abelian group, then, for all a, b in A, the equivalence(a o b) o ... o (a o b)n times = (a o ... o a)n times o (b o ... o b)n times
... On the other hand, instead of a book, imagine a proof development system for algebra; there the theorem cannot be stated, since it is not a theorem of abelian group theory, it is, rather, a meta-theorem, a theorem about abelian group theory.
But all this is from the completely irrelevant perspective of an axiomatization
of group theory in first order logic. As we have already stated, any serious
development of group theory is going to use higher-order or set-theoretic
devices, as Bourbaki does for example. With these mathematical resources,
iterated operations are trivially definable and their basic properties easily
provable --- this appears right at the very beginning of the well-known algebra
textbook of [lang-algebra] for example, and in section 1.4 of
[jacobson1]! The stress on direct first order axiomatizations in the AI
community probably results from a laudable scepticism in some quarters towards
the fancy new logics being promulgated by others, but it completely fails to
reflect real mathematical practice. What is true is that one often sees
statements like 'the other cases are similar' or 'by symmetry we may assume
that m 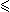 n'. These have the flavour of metatheorems in that they relate
similar proofs rather than theorems. But bear in mind that when
presenting proofs informally, this is just one of many devices used to
abbreviate them. Certainly, a way of formalizing statements like this is as
metatheorems connecting proofs. But another is simply to do (or program the
computer to do!) all the cases explicitly, or to use an object-level theorem
directly as justification, e.g.
n'. These have the flavour of metatheorems in that they relate
similar proofs rather than theorems. But bear in mind that when
presenting proofs informally, this is just one of many devices used to
abbreviate them. Certainly, a way of formalizing statements like this is as
metatheorems connecting proofs. But another is simply to do (or program the
computer to do!) all the cases explicitly, or to use an object-level theorem
directly as justification, e.g.
( m, n. P(m,n)
m, n. P(m,n)  P(n,m))
P(n,m))  ((
(( m, n. P(m,n))
m, n. P(m,n))  (
( m, n. m
m, n. m 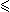 n
n  P(m,n))
P(m,n))
Performing similar proofs in different contexts may anyway be a hint that one should be searching for a suitable mathematical generalization to include all the cases.
So, we have yet to find the LCF approach inadequate, and yet to see really useful implementations of reflection. Whatever exotic principles are added, the provable sentences will form a recursively enumerable set (we are after all considering a computer implementation), and once again there will be unprovable statements and infeasible ones. Now since we haven't come across any interesting infeasible statements yet it seems extremely conjectural that they won't still be infeasible in the expanded system. Boyer reports that the metafunction facility of NQTHM is not widely used in practice, even though it is the only way for an ordinary user to add new facilities to NQTHM. And [constable-programs], who are no enemies of the idea of reflection as indicated by their extensive writings on the subject, say: 'Of all these methods [of providing extensibility] we have found the LCF idea easiest to use and the most powerful.'



 John Harrison
96/8/13; HTML by
John Harrison
96/8/13; HTML by  96/8/16
96/8/16