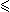 X, or to distinguish between a
function and its value. But it may be that the accumulation of such details
renders mathematics too inelegant. Only experience can tell.
X, or to distinguish between a
function and its value. But it may be that the accumulation of such details
renders mathematics too inelegant. Only experience can tell.


There has already been considerable experience of formalized mathematics in widely differing theorem proving systems. It's important to absorb the lessons this yields about the process in general, and the strengths and weaknesses of particular formal systems and proof methodologies. Most of the following is based on personal experience, but we feel that much of it will be echoed by other practitioners.
Formalizing mathematics is sometimes quite difficult. It's not uncommon to make a definition, set about proving some consequences of it, fail, and then realize that the definition was faulty. Usually this is because some trivial degenerate case was ignored, sometimes because of a more substantive misunderstanding. This can be tedious, but at other times it is clarifying, and forces one to think precisely.
It's an interesting question whether modest changes to normal mathematical
style can render mathematics completely formal, or whether this will always be
an unbearably tedious load (some say that 'rigour means rigor mortis'). It
certainly doesn't seem too much trouble always to say explicitly that p is a
prime, that n is a natural number, that when we talk about the poset X we
are talking about the partial order 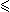 X, or to distinguish between a
function and its value. But it may be that the accumulation of such details
renders mathematics too inelegant. Only experience can tell.
X, or to distinguish between a
function and its value. But it may be that the accumulation of such details
renders mathematics too inelegant. Only experience can tell.
Formal proofs can be long and tedious, and tend to look quite unreadable compared with their textbook models. However we believe several existing systems such as Mizar show that one can still provide fairly readable proof texts, and the main difficulty in practice is automating just the right parts of the reasoning. In principle, there seems no reason why proofs cannot be brought down to something close to the length of textbook ones; even less perhaps. Of course, for a few exceptionally explicit and precise textbooks, this may already be the case.
In any case (though this comment might seem to smack of desperation) there are advantages in the fact that proofs are more difficult. One tends to think more carefully beforehand about just what is the best and most elegant proof. One sees common patterns that can be exploited. All this is valuable. Compare the greater care one would take when writing a book or essay in the days before word processors.
In practice formalized mathematics is quite addictive (at least, for a certain kind of personality). This may be similar to the usual forms of computer addiction, but we believe there is another important factor at work. Since one can usually see one's way intuitively to the end of the proof, one has a continual mirage before one's eyes, an impression of being almost there! This must account for the times people stay up till the small hours of the morning trying to finish 'just one last proof'. Moreover, the continual computer feedback provides a stimulus, and the feeling of complete confidence that each step is correct helps dispel any feelings that the undertaking is futile since mistakes will have been made anyway.
Many of the problems are not connected with the profound and interesting difficulties of formalizing and proving things, but with the prosaic matter of organizing the resulting database of theorems. Since one will often need to refer back to previous theorems, possibly proved by other people, it's useful to have a good lookup technique. In mathematics texts, readers can only remember a few 'big names' like the Heine-Borel theorem, the Nullstellensatz, and the rather ironic relic of 'Hilbert's Theorem 90' which in retrospect needed a name! For run of the mill theorems, it's better to number them: although the numeration scheme may be without significance, it does at least facilitate relatively easy lookup (though some books unhelpfully adopt distinct numbering streams for theorems, lemmas, corollaries and definitions). Mizar numbers its theorems, though inside textual units which are named. But this policy seems to us less suitable for a computer theorem prover because it's more common to want to pass from a (fancied) theorem to its identifier, rather than vice versa. Admittedly in the long term we want people to read formal proofs, but at present the main emphasis on constructing them. Still, we want to bear in mind the convenience of a later reader or user as well as the writer.
With a computer system, textual lookup is at least as easy as numeric lookup, and names can have a mnemonic value, so using names throughout seems a better choice. It also makes it easier to insert or rearrange theorems without destroying any logic in the naming scheme. HOL names all theorems, but some theories do not have a consistent naming convention, notably natural number arithmetic which used to include the aptly-named TOTALLY_AD_HOC_LEMMA. A computer can offer the new possibility of looking up a theorem according to its structure, e.g. finding a theorem that will match a given term, or contains a certain combination of constants. HOL and IMPS have such facilities.
Then there are the social problems: when different people work at formalizing
mathematics, they will choose slightly different conventions, and perhaps
reinvent the same concepts with different names. For example, one may take <
as the basic notion of ordering, one may take 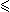 (or > or
(or > or  ).
Perhaps there needs to be some kind of central authority (like the Mizar
'library committee') which establishes certain canons, but this is rife with
potential for disagreement and petty politicking. We should reiterate our
earlier remarks here: there are real advantages in only allowing users one way
to do things! If different users prove the same results at different level of
generality, this is less likely to lead to ideological division. However there
may be no generally agreed 'most abstract' form of a given result, and even if
this can be agreed on, the task of integrating the two theories may not be
trivial. Sometimes it may be most natural to prove a result at different levels
of generality, for reasons of logical dependency. For example, Gauss' proof
that if a ring R is a unique factorization domain then so is its polynomial
ring R[x], uses as a lemma the fact that the ring of polynomials over a field
is a UFD; this lemma is however a special case of the main result.
).
Perhaps there needs to be some kind of central authority (like the Mizar
'library committee') which establishes certain canons, but this is rife with
potential for disagreement and petty politicking. We should reiterate our
earlier remarks here: there are real advantages in only allowing users one way
to do things! If different users prove the same results at different level of
generality, this is less likely to lead to ideological division. However there
may be no generally agreed 'most abstract' form of a given result, and even if
this can be agreed on, the task of integrating the two theories may not be
trivial. Sometimes it may be most natural to prove a result at different levels
of generality, for reasons of logical dependency. For example, Gauss' proof
that if a ring R is a unique factorization domain then so is its polynomial
ring R[x], uses as a lemma the fact that the ring of polynomials over a field
is a UFD; this lemma is however a special case of the main result.
And in practice, a given arrangement is not set in stone; people may want to add more theorems to existing libraries, perhaps slightly modify the theorems on which other libraries depend. It seems that making minor changes systematically should become easier with computer assistance, just as making textual changes becomes easier with word processing software. But sometimes it does prove to be very difficult --- the problem has been studied by [curzon-changes] with respect to large hardware verification proofs. How much worse if we want to change the foundational system more radically (e.g. constructivists might like to excise the use of nonconstructive principles in proofs). It seems that a suitably 'declarative' proof style is the key, and one should try to write proofs which avoid too many unnecessary parochial assumptions (e.g. the assumption that there are von Neumann ordinals floating around). This is comparable to avoiding machine dependencies in programming.



 John Harrison
96/8/13; HTML by
John Harrison
96/8/13; HTML by  96/8/16
96/8/16