

The choice of a foundational system
As already indicated, the intellectual trend has in the past moved away from
the idea of actually using formal systems towards using them at one remove.
This is responsible for the almost exclusive concentration on first order
logic, despite its obvious defects.31 In
general we should not be awed by existing foundational systems (as Kant was by
Aristotelean logic) but should be prepared to invent our own new ideas. Even
quite trivial syntactic changes, like making quantifiers bind more weakly than
other connectives (most logic books adopt the opposite convention) can help
with the usability of the system!
There are two major foundational schemes for mathematics: set theory and type
theory. These can be traced back to Zermelo and Russell, respectively, and to
their different reactions to the paradoxes of naive set theory. Zermelo felt
that the Russell set {x | x 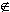 x} was paradoxical because (since so
many sets don't have the property x
x} was paradoxical because (since so
many sets don't have the property x  x) it was simply too big
to be a set. Indeed, Cantor had already distinguished between 'consistent' and
'inconsistent' multiplicities, more or less on the basis of size (whether they
were equinumerous with the class of all ordinals). This is called the
'limitation of size' doctrine. Russell, on the other hand, felt that the
problem was with the circular nature of the definition (considering whether a
set is a member of itself), and proposed separating mathematical objects into
layers, so that it only makes sense to ask whether an object at layer n is a
member of an object of layer n + 1, making the Russell set meaningless on
syntactic grounds.
x) it was simply too big
to be a set. Indeed, Cantor had already distinguished between 'consistent' and
'inconsistent' multiplicities, more or less on the basis of size (whether they
were equinumerous with the class of all ordinals). This is called the
'limitation of size' doctrine. Russell, on the other hand, felt that the
problem was with the circular nature of the definition (considering whether a
set is a member of itself), and proposed separating mathematical objects into
layers, so that it only makes sense to ask whether an object at layer n is a
member of an object of layer n + 1, making the Russell set meaningless on
syntactic grounds.
In fact the distinction between set theory and type theory is not clear-cut.
Fraenkel added the Axiom of Foundation to Zermelo's set theory, and this gave
rise to an intuitive picture of the set-theoretic universe as built up layer by
layer in a wellfounded way. (A picture which is nowadays de rigeure
among set theorists, and even presented as the motivation for the ZF axioms!)
This really amounts to an admixture of type theory, although the layers are
cumulative (each layer includes the previous one) and continued transfinitely.
What's more, Quine has proposed set theories which, while not having a global
notion of type, have a kind of local type discipline based on stratified
formulas in the comprehension schema. On the other hand, it seems that
Martin-Löf, one of the standard-bearers of type theory, now prefers to refer
to his systems as 'Martin-Löf set theory'.
We can still perhaps distinguish types in that they render ill-typed phrases
meaningless, whereas ZF set theory, say, merely makes them false.
(For ZF set theory, we mean by 'ill-typed' statements of the form s  t
where s has a rank in the cumulative hierarchy at least as great as t,
rather than those ill-typed in a more intuitive sense.) Moreover, typing
judgements have traditionally been syntactic, or more precisely, decidable. For
simple type theory, not only typechecking, but type inference, is automatic:
the Hindley-Milner algorithm generates a most general type for any typable
expression. However this usually fails for more complex type theories, e.g.
PVS's; even type checking can be undecidable in certain dependent type
theories.
t
where s has a rank in the cumulative hierarchy at least as great as t,
rather than those ill-typed in a more intuitive sense.) Moreover, typing
judgements have traditionally been syntactic, or more precisely, decidable. For
simple type theory, not only typechecking, but type inference, is automatic:
the Hindley-Milner algorithm generates a most general type for any typable
expression. However this usually fails for more complex type theories, e.g.
PVS's; even type checking can be undecidable in certain dependent type
theories.
Types also arose, perhaps at first largely independently of Russellian
foundational schemes, in programming languages. In general we may say that
types impose additional layers of structure. Even FORTRAN distinguished
integers and floating point values. One reason was clearly efficiency: the
machine can generate more efficient code, and use storage more effectively, by
knowing more about a variable. For example the implementation of C's pointer
arithmetic varies according to the size of the referenced objects. If p is a
pointer to objects occupying 4 bytes, then what C programmers write as p +
1 becomes p + 4 inside the (byte-addressed) machine. C's ancestor BCPL was
untyped, and was therefore unable to distinguish pointers from integers; to
support the same style of pointer arithmetic it was necessary to apply a
scaling at every indirection, a significant penalty. Apart from efficiency, as
time went by, types also began to be appreciated more and more for their value
in providing limited static checks (i.e. checks that can be made before running
the program) on program correctness and for achieving modularization and data
hiding. It seems that types might offer at least these advantages to pure
mathematics too. For automated theorem proving there may even be comparable
efficiency advantages, since types can be used to direct proof search and avoid
considering 'nonsensical' combinations of terms. From a practical point of
view, one appeal of type theory is that the rendering of higher-level
mathematical notions like functions is rather direct, whereas in set theory it
relies on a few layers of definition. There seems a well-established view that
type theory is in some ways a more natural vehicle for mathematics. For
example, [hilbert-ackermann] assert that 'the calculus of order \omega
is the appropriate means for expressing the modes of inference of mathematical
analysis'. Such a system, more usually known as simple type theory, is
considered below.
We will concentrate on such practicalities of set theory and type theory
as foundations, but it's worth pausing a while to examine the matter
philosophically. It seems that there really is a notion of type at work in
everyday mathematics; we do think of real numbers as something different from
sets of complex numbers, and flattening the whole universe of mathematical
discourse into a single undifferentiated realm doesn't seem natural. However
the same can be said of any reductive foundationalist programme. In any case,
whatever the intuitive appeal of types, ZFC seems to indicate that they are not
necessary to ensure consistency.32 There are other special
attributes that mathematical objects may have, and 'type' should perhaps just
be one of these. Types as primitive can also present awkward choices over
whether to formalize some set as a new type or as a subset of (or predicate on)
an existing type. In any kind of collaborative programme, it's good policy to
avoid giving people too many unnecessary choices (the C programming language
and the Macintosh user interface both reflect this philosophy). While on the
subject of programming, we might say that however one uses a type discipline in
a high-level programming language, it's all implemented using machine code,
which is almost completely untyped. Similarly, we might regard set theory as an
underlying machine code to which statements with higher levels of structure may
be 'compiled'.
Simple type theory (higher order or \omega-order logic) is a direct
descendant of Russell's type theory, as simplified by [chwistek],
[ramsey-fm] and [church-types]. It is successfully implemented in
SAM V [guard-sam], TPS [andrews-tps] and, with the addition of a form
of polymorphism, in HOL [gordon-holbook]. True to its name, simple type
theory is a simple system, formally and conceptually. In fact, only a
higher-order equational calculus with 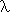 -binding need be taken as basic;
as shown by [henkin-ptypes], all the logical operations can be defined as
higher order functions given some 2-element type of
propositions.33 The resulting system is in many ways quite close to
informal mathematics; the types are often helpful and natural, and functions
are first-class objects. However it is rather inflexible in some ways; for
example there are no dependent types (where a type depends on a term, e.g. a
type of n
-binding need be taken as basic;
as shown by [henkin-ptypes], all the logical operations can be defined as
higher order functions given some 2-element type of
propositions.33 The resulting system is in many ways quite close to
informal mathematics; the types are often helpful and natural, and functions
are first-class objects. However it is rather inflexible in some ways; for
example there are no dependent types (where a type depends on a term, e.g. a
type of n  n matrices for variable n). So although convenient for
some parts of mathematics (particularly concrete situations like number theory
and real analysis), it becomes rather inflexible for other parts, e.g. abstract
algebra. However some objections often made to type theory are rather specious.
For example, it's true that R and N are completely different types
in simple type theory, but there are subtyping schemes which can make N
n matrices for variable n). So although convenient for
some parts of mathematics (particularly concrete situations like number theory
and real analysis), it becomes rather inflexible for other parts, e.g. abstract
algebra. However some objections often made to type theory are rather specious.
For example, it's true that R and N are completely different types
in simple type theory, but there are subtyping schemes which can make N
 R; in any case this inclusion also fails in the standard
set-theoretic development of the reals. Moreover, one can perfectly well do
limited set-theoretic reasoning within a fixed 'universe' type in type theory
simply by using predicates.
R; in any case this inclusion also fails in the standard
set-theoretic development of the reals. Moreover, one can perfectly well do
limited set-theoretic reasoning within a fixed 'universe' type in type theory
simply by using predicates.
There are plenty of more advanced type theories which allow dependent types and
other more sophisticated type constructors. Many of these are descended from
Martin-Löf's constructive type theories, which are based on the Curry-Howard
correspondence between propositions and types (type constructors correspond to
logical operators, e.g. the product type to conjunction). However there is no
reason why these systems cannot be used classically. It seems that they are
much more flexible than simple type theory, but they are also much more
complicated. For example, Nuprl's type theory has over 200 inference rules,
although the Calculus of Constructions and related systems are much simpler.
Quite how easy it is to formalize mathematics in these systems is still an open
question. Many of the researchers are also constructivists, and it is not easy
to separate the peculiarities of using constructive logic from the
peculiarities of using type theory. There are a number of interesting research
projects under way in this line. For example [huet-saibi] have been
investigating category theory, notoriously hard to formalize in any kind of
system, in the Calculus of Constructions.
Set theory (e.g. ZFC) is probably the most obvious choice as a foundation. It
isn't as simple as simple type theory, and as our earlier remarks indicate, is
a rather ad hoc solution to the paradoxes. However it is reasonably simple, and
appears to be flexible enough for just about all present-day mathematics.
Importantly, it is much better known among mathematicians than type
theory.34 There are still question marks over its suitability, even with
additional axioms, for some parts of category theory (the category of all sets,
etc.) Moreover, if the system is based on first order logic, some theorems such
as recursion on a wellfounded relation need to be stated in an artificial
manner using devices such as proper classes. There are no types to hinder us,
but none to help us either. In practice it seems likely that some quite simple
abbreviations for set constraints are sufficient to give most of the
convenience of types, without irrevocably tying the user to them.
The exact set theory to choose is open to debate. The 'standard' foundation for
mathematics is ZFC based on first order logic. However basing the system on
higher order logic brings some advantages. Notably, one can express axioms like
Replacement as Zermelo thought of them informally, rather than via artificial
first order paraphrases. [carnap-symlog] presents set theory in this way,
and even shows how using a second order quantifier one can express Fraenkel's
'Axiom of Restriction' in a direct way. Recently [gordon-st] has
axiomatized such a higher order set theory in the HOL prover. Since one can use
higher order bound variables in axiom schemas, this gives a properly stronger
theory than first order ZF. However this can be avoided in several ways while
still retaining some of the convenience of higher order logic. For example
Mizar uses first order logic with free second order variables ('1.001 order
logic'), which does at least render axioms schemas more pleasant to deal with.
[corella-thesis] restricts the ZF axioms to their first order forms and
proves that this is a conservative extension of first order ZF, while
nevertheless allowing some attractive higher order features (e.g. uniformity of
definitional mechanisms).
There is also the possibility of retaining first order logic, but making
classes first-class objects, as in NBG. Some descendants of Quine's set
theories include something similar to the ZF universe of sets, while providing
some convenient additional facilities like a set universe which is a Boolean
algebra [holmes-naive]. Finally, it is possible to add extra axioms, e.g.
the Tarski-Grothendieck axiom of universes,35 or take them away --- for example Replacement is seldom used in
mainstream mathematics.36 Mizar settled on
Tarski-Grothendieck set theory, after a few experiments with Morse-Kelley. This
latter theory, by the way, was the basis for an unusually formal but very
elegant book by [morse-sets]; the present author been told that Morse
used this formalism in his teaching and research in analysis. It is also
familiar to many practising pure mathematicians, as it was presented as an
appendix to the classic topology textbook by [kelley].
Of course, it is possible to combine features of type theory and set theory.
For example, the work of [gordon-st] already mentioned includes some
experimental features to link the two. [agerholm-dinf] has formalized the
construction of the D fty model of untyped
fty model of untyped 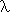 -calculus in
Gordon's combined system, something very hard to do in (simple) type theory
alone. A more radical solution is to make some of the theorem-proving
facilities generic, allowing the use of the prover for set theory, type
theory, and other logics too. For example, Isabelle [paulson-isabellebook]
includes some fairly powerful proof tools which are applicable to various
logics. It has been used for quite extensive developments of simple type
theory and first order ZF set theory.
-calculus in
Gordon's combined system, something very hard to do in (simple) type theory
alone. A more radical solution is to make some of the theorem-proving
facilities generic, allowing the use of the prover for set theory, type
theory, and other logics too. For example, Isabelle [paulson-isabellebook]
includes some fairly powerful proof tools which are applicable to various
logics. It has been used for quite extensive developments of simple type
theory and first order ZF set theory.
We can judge a foundational system by several criteria: aesthetic and
philosophical appeal, flexibility, simplicity and closeness to ordinary
mathematical language. These are partly subjective of course. And unfortunately
many of them, especially the last two, tend to be in conflict. It seems that
at present set theory is the winner, but with more research on different
foundational systems, this may change. We do not believe the last word has been
said.



 John Harrison
96/8/13; HTML by
John Harrison
96/8/13; HTML by  96/8/16
96/8/16
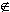 x} was paradoxical because (since so
many sets don't have the property x
x} was paradoxical because (since so
many sets don't have the property x  x) it was simply too big
to be a set. Indeed, Cantor had already distinguished between 'consistent' and
'inconsistent' multiplicities, more or less on the basis of size (whether they
were equinumerous with the class of all ordinals). This is called the
'limitation of size' doctrine. Russell, on the other hand, felt that the
problem was with the circular nature of the definition (considering whether a
set is a member of itself), and proposed separating mathematical objects into
layers, so that it only makes sense to ask whether an object at layer n is a
member of an object of layer n + 1, making the Russell set meaningless on
syntactic grounds.
x) it was simply too big
to be a set. Indeed, Cantor had already distinguished between 'consistent' and
'inconsistent' multiplicities, more or less on the basis of size (whether they
were equinumerous with the class of all ordinals). This is called the
'limitation of size' doctrine. Russell, on the other hand, felt that the
problem was with the circular nature of the definition (considering whether a
set is a member of itself), and proposed separating mathematical objects into
layers, so that it only makes sense to ask whether an object at layer n is a
member of an object of layer n + 1, making the Russell set meaningless on
syntactic grounds.


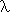 -binding need be taken as basic;
as shown by
-binding need be taken as basic;
as shown by  n matrices for variable n). So although convenient for
some parts of mathematics (particularly concrete situations like number theory
and real analysis), it becomes rather inflexible for other parts, e.g. abstract
algebra. However some objections often made to type theory are rather specious.
For example, it's true that R and N are completely different types
in simple type theory, but there are subtyping schemes which can make N
n matrices for variable n). So although convenient for
some parts of mathematics (particularly concrete situations like number theory
and real analysis), it becomes rather inflexible for other parts, e.g. abstract
algebra. However some objections often made to type theory are rather specious.
For example, it's true that R and N are completely different types
in simple type theory, but there are subtyping schemes which can make N
 R; in any case this inclusion also fails in the standard
set-theoretic development of the reals. Moreover, one can perfectly well do
limited set-theoretic reasoning within a fixed 'universe' type in type theory
simply by using predicates.
R; in any case this inclusion also fails in the standard
set-theoretic development of the reals. Moreover, one can perfectly well do
limited set-theoretic reasoning within a fixed 'universe' type in type theory
simply by using predicates.

 John Harrison
96/8/13; HTML by
John Harrison
96/8/13; HTML by  96/8/16
96/8/16