

Definitions and locutions
In practice, even in quite rich foundational systems, let alone in pure set
theory, representations of mathematical objects become unwieldy. For example,
[bourbaki-sets] estimates37 that even the number 1 if fully expanded would occupy
thousands of symbols in his system. So some kind of definitional mechanism is
needed, at least for human consumption, and possibly to stop overflow even for
a machine! The fundamental property of definitions is that it should be
possible in principle to do without them, though we need to say precisely what
this means.
The simplest kinds of definitions are just shorthands for more complicated
expressions, for example 2 rather than {0,1}, (x,y) rather
than {x,{x,y}} and  !x. P[x] rather than
!x. P[x] rather than  x. P[x]
x. P[x] 
 y. P[y]
y. P[y]  y = x. We can understand such definitions in two ways,
either as metalogical abbreviations used to make formal texts more palatable to
the reader, or as a method of sanctioning the addition (in the object logic) of
new equational axioms. Generally, the latter is more efficient, since it keeps
the underlying terms small, but the former is more flexible: the defined notion
need not correspond to any kind of logical object, nor respect any underlying
type system. In fact the Nuprl system allows boths kinds of definition.
y = x. We can understand such definitions in two ways,
either as metalogical abbreviations used to make formal texts more palatable to
the reader, or as a method of sanctioning the addition (in the object logic) of
new equational axioms. Generally, the latter is more efficient, since it keeps
the underlying terms small, but the former is more flexible: the defined notion
need not correspond to any kind of logical object, nor respect any underlying
type system. In fact the Nuprl system allows boths kinds of definition.
Assuming that the object language has facilities for variable abstraction
(something like lambda-calculus), then any definitional constructs of this kind
can be reduced to new abbreviations or axioms of the form c = t where c
is a new constant name any t any closed term. For example, instead of writing
f(x) = E[x], we use f = 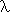 x. E[x]. In any reasonable logical system the
addition of such axioms makes no difference: in principle we could do without
them (replace c by its expansion everywhere), and we do not derive any new
facts not mentioning c. They thus fulfil all the criteria we could demand of
definitions.
x. E[x]. In any reasonable logical system the
addition of such axioms makes no difference: in principle we could do without
them (replace c by its expansion everywhere), and we do not derive any new
facts not mentioning c. They thus fulfil all the criteria we could demand of
definitions.
There is a more general means of extending the logic with new constant symbols:
using names for things which have been proved to exist. If we can prove 
 x. P[x], then adding a new constant c and an axiom
x. P[x], then adding a new constant c and an axiom  P[c] is a
conservative extension of most logical systems, in the sense that anything not
involving c could equally well be deduced without using c or its axiom.
(Simply because something like the natural deduction
P[c] is a
conservative extension of most logical systems, in the sense that anything not
involving c could equally well be deduced without using c or its axiom.
(Simply because something like the natural deduction  -elim rule is
usually valid.) It's not quite conservative in the sense that it can be written
away from formulas, though any formula Q[c] can be read as (
-elim rule is
usually valid.) It's not quite conservative in the sense that it can be written
away from formulas, though any formula Q[c] can be read as ( x. P[x])
x. P[x])

 x. P[x]
x. P[x]  Q[x], for example. Given a theorem
Q[x], for example. Given a theorem 
 x.
x.
 !y. P[x,y], it is usually conservative to add a new function symbol f
and an axiom
!y. P[x,y], it is usually conservative to add a new function symbol f
and an axiom 
 x. P[x,f(x)]. However if unique existence is
weakened to existence, this can smuggle in the Axiom of Choice. The situation
for constructive logics is even more delicate.
x. P[x,f(x)]. However if unique existence is
weakened to existence, this can smuggle in the Axiom of Choice. The situation
for constructive logics is even more delicate.
A useful feature in a practical logic is a descriptor. For example, we
may allow a new term constructor  x. P[x] ('the (unique) x such that
P[x]'), together with an axiom
x. P[x] ('the (unique) x such that
P[x]'), together with an axiom  (
( !x. P[x])
!x. P[x])  P[
P[ x.
P[x]], or
x.
P[x]], or 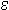 x. P[x] ('some x such that P[x]'), together with an
axiom
x. P[x] ('some x such that P[x]'), together with an
axiom  (
( x. P[x])
x. P[x])  P[
P[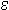 x. P[x]]. These are called definite
and indefinite descriptors, respectively. Note that the latter is something
like the Axiom of Global Choice if we allow P[x] to contain other free
variables, and even the former is weakly nonconstructive because it effectively
allows us to introduce a total function even though
x. P[x]]. These are called definite
and indefinite descriptors, respectively. Note that the latter is something
like the Axiom of Global Choice if we allow P[x] to contain other free
variables, and even the former is weakly nonconstructive because it effectively
allows us to introduce a total function even though  x. P[x] may be
conditional on some other property. For this reason descriptors in formal
presentations of constructive logic [troelstra-con1] are usually partial
operators --- this topic is discussed below.
x. P[x] may be
conditional on some other property. For this reason descriptors in formal
presentations of constructive logic [troelstra-con1] are usually partial
operators --- this topic is discussed below.
A descriptor is very useful for rendering informal notions of 'the x such
that ...' (it's much used by Bourbaki), and can even be used to implement
lambda-binding, set abstraction and so on, e.g. define 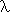 x. E[x] to be
x. E[x] to be
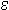 f.
f.  x. f(x) = E[x]. If we have
x. f(x) = E[x]. If we have 
 x. P[x] and we have
an indefinite descriptor, then defining c =
x. P[x] and we have
an indefinite descriptor, then defining c = 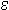 x. P[x] gives us
x. P[x] gives us  P[c]. Conversely, for any term t we have
P[c]. Conversely, for any term t we have 
 x. x = t, so the
existential kind of definition always sanctions the equational kind. There is
thus a close relationship between the two kinds of definition, given a
descriptor.
x. x = t, so the
existential kind of definition always sanctions the equational kind. There is
thus a close relationship between the two kinds of definition, given a
descriptor.
There are more complex definitional mechanisms which cannot be expanded away in
such a simple-minded manner, but can nevertheless be understood as inessential
abbreviations that could in principle be done without. These are usually
referred to as contextual definitions. A good example is the use of ZF
proper classes, where set-like statements about classes are really encoded
using logical predicates. Another example: cardinal numbers can in principle be
done without for most purposes, since all statements about arithmetic and
equality of cardinals may be regarded as statements about equinumerosity etc.
of sets. For example instead of |X| = |Y|2 |Z| we can write 'there is a
bijection between X and (Y 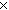 Y)
Y) 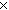 Z'. The most sophisticated
example of all is using category-theoretic language like 'the category of all
sets' purely as a syntactic sugar on top of quite different statements. One of
the interesting questions in formalized mathematics is the extent to which this
is possible.
Z'. The most sophisticated
example of all is using category-theoretic language like 'the category of all
sets' purely as a syntactic sugar on top of quite different statements. One of
the interesting questions in formalized mathematics is the extent to which this
is possible.
In any case, we shouldn't lay too much stress on the theoretical
eliminability of definitions. It's mainly a way of assuring ourselves
that we aren't 'really' extending the logic. Life without definitions would be
unbearably complicated, and anyway the whole significance of a theorem may
subsist in the definitions it depends on.
There are other forms of definition, for example definition by recursion and
definition of inductive sets or relations. However given a mathematical theorem
justifying the existence of such a function, it can then be defined using one
of the mechanisms given above. In programmable systems, the tedious matter of
deriving the required case of this theorem can be automated completely.



 John Harrison
96/8/13; HTML by
John Harrison
96/8/13; HTML by  96/8/16
96/8/16
 !x. P[x] rather than
!x. P[x] rather than  x. P[x]
x. P[x] 
 y. P[y]
y. P[y]  y = x. We can understand such definitions in two ways,
either as metalogical abbreviations used to make formal texts more palatable to
the reader, or as a method of sanctioning the addition (in the object logic) of
new equational axioms. Generally, the latter is more efficient, since it keeps
the underlying terms small, but the former is more flexible: the defined notion
need not correspond to any kind of logical object, nor respect any underlying
type system. In fact the Nuprl system allows boths kinds of definition.
y = x. We can understand such definitions in two ways,
either as metalogical abbreviations used to make formal texts more palatable to
the reader, or as a method of sanctioning the addition (in the object logic) of
new equational axioms. Generally, the latter is more efficient, since it keeps
the underlying terms small, but the former is more flexible: the defined notion
need not correspond to any kind of logical object, nor respect any underlying
type system. In fact the Nuprl system allows boths kinds of definition.


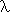 x. E[x]. In any reasonable logical system the
addition of such axioms makes no difference: in principle we could do without
them (replace c by its expansion everywhere), and we do not derive any new
facts not mentioning c. They thus fulfil all the criteria we could demand of
definitions.
x. E[x]. In any reasonable logical system the
addition of such axioms makes no difference: in principle we could do without
them (replace c by its expansion everywhere), and we do not derive any new
facts not mentioning c. They thus fulfil all the criteria we could demand of
definitions.

 x. P[x] ('the (unique) x such that
P[x]'), together with an axiom
x. P[x] ('the (unique) x such that
P[x]'), together with an axiom 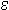 x. P[x] ('some x such that P[x]'), together with an
axiom
x. P[x] ('some x such that P[x]'), together with an
axiom 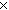 Y)
Y) 
 John Harrison
96/8/13; HTML by
John Harrison
96/8/13; HTML by  96/8/16
96/8/16