

Partial functions and undefined terms
In informal mathematics, our minds filter out (subconsciously?) troublesome
degenerate cases. However in a formal treatment we must address these matters.
One of the most interesting questions is: what does it mean to apply a function
f to a value x outside its domain? For example, what is 0-1 in the
reals?
There are numerous different approaches. The simplest is to regard f(x) for
x 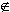 dom(f) as something arbitrary; in effect we are expanding the
domain of f but saying nothing about the values it takes there.
Alternatively, we can specify an explicit value for arguments outside the
domain; this approach can be exploited by choosing a particularly convenient
one. For example, if we decide 0-1 = 0, we have lots of nice unconditional
theorems, like
dom(f) as something arbitrary; in effect we are expanding the
domain of f but saying nothing about the values it takes there.
Alternatively, we can specify an explicit value for arguments outside the
domain; this approach can be exploited by choosing a particularly convenient
one. For example, if we decide 0-1 = 0, we have lots of nice unconditional
theorems, like  x
x  R. (x-1)-1 = x,
R. (x-1)-1 = x,  x
x  R.
-x-1 = (-x)-1,
R.
-x-1 = (-x)-1,  x, y
x, y  R. (x y)-1 = x-1 y-1 and
R. (x y)-1 = x-1 y-1 and
 x
x  R. x-1
R. x-1  0
0  x
x  0. However some may regard these
theorems as pathological, obscene or simply untrue. Actually even if an
arbitrary value is chosen, these freak theorems show up occasionally. If we
define, as one normally would, x / y = x y-1, then 0 / 0 = 0, because
whatever 0-1 might be, it's some real number, and multiplying it by zero
gives zero! In an untyped system this problem happens less (in the example
given we wouldn't even know that 0-1
0. However some may regard these
theorems as pathological, obscene or simply untrue. Actually even if an
arbitrary value is chosen, these freak theorems show up occasionally. If we
define, as one normally would, x / y = x y-1, then 0 / 0 = 0, because
whatever 0-1 might be, it's some real number, and multiplying it by zero
gives zero! In an untyped system this problem happens less (in the example
given we wouldn't even know that 0-1  R), but does not disappear
completely.
R), but does not disappear
completely.
There is a more serious disadvantage of this scheme. (In constructive systems
there is yet another: membership of the domain may be undecidable, so the above
solution simply isn't available.) In some mathematical contexts, writing down
f(x) = y is taken to include an implicit assertion that x  dom(f). For
example, when we write:
dom(f). For
example, when we write:
 x. d/(dx) sin(x) = cos(x)
x. d/(dx) sin(x) = cos(x)
we take this to include an assertion that sin is in fact
differentiable everywhere. But if the differentiation operator is total, it
will yield a value, regardless of whether the function is actually
differentiable at the relevant point. It might accidentally happen that the
above equation were true even if the function weren't differentiable! Hence an
equation like the above contains less information than one would intuitively
expect. This situation becomes even more serious when such constructs are
nested, e.g. in differential equations. They need to be accompanied by a long
string of differentiability assumptions, which in informal usage are understood
implicitly. Again, this is less of a problem in set theory; one might for
example adopt the convention of extending partial functions X  Y to total
functions X
Y to total
functions X  Y
Y  Y, using the value Y to denote undefinedness.
Y, using the value Y to denote undefinedness.
What are the alternatives? If we have a typed logic, then we can simply make
f(x) a typing error when x 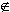 dom(f); that is, the term is not
syntactically well formed. This avoids the problems above, but it might mean
that in certain situations in analysis, the types become complicated, since
they need to excise all the singularities. It also makes it difficult to use
constructs which are permissive of point singularities (for example, it often
makes sense to integrate such functions). Moreover, the truth of certain
theorems such as
dom(f); that is, the term is not
syntactically well formed. This avoids the problems above, but it might mean
that in certain situations in analysis, the types become complicated, since
they need to excise all the singularities. It also makes it difficult to use
constructs which are permissive of point singularities (for example, it often
makes sense to integrate such functions). Moreover, the truth of certain
theorems such as  x
x  R. tan(x) = 0
R. tan(x) = 0 
 n
n  Z. x = n
Z. x = n  depend on quite small details of how the typechecking and basic logic interact.
depend on quite small details of how the typechecking and basic logic interact.
The most sophisticated alternative of all is to have a special logic which
allows certain terms to be undefined, as in the IMPS system [farmer-imps].
This is more or less the same (there are some differences in detail) as taking
an extra 'undefined' element on top of a conventional logic, so the result of a
function application may be this special element.38 The undefined value
propagates up through terms, so a term with an undefined subterm is itself
undefined. In IMPS, predicates involving an undefined argument become
false. For example, a = b means 'a and b are both defined and are
equal'. One might question these choices, but since a definedness operator is
provided, one can invent one's own bespoke notion of equality. In particular,
IMPS supports 'quasi-equality', where a = b means 'either a and b are
both undefined, or are both defined and equal'. In some parts of mathematics,
this is probably the usual convention, but it has some surprising consequences,
e.g. the logical equivalence s = t  s - t = 0 is false for quasi-equality
for certain terms s and t. One could even imagine circumstances in which
s - t = 0 is false for quasi-equality
for certain terms s and t. One could even imagine circumstances in which
 x
x  R. (x2 - 1) / (x - 1) = x + 1 was desired behaviour (wherever
the two sides are both defined, they are equal). Actually,
[freyd-allegories] use a special asymmetric 'Venturi tube' equality
meaning 'if the left is defined then so is the right and they are equal'.
R. (x2 - 1) / (x - 1) = x + 1 was desired behaviour (wherever
the two sides are both defined, they are equal). Actually,
[freyd-allegories] use a special asymmetric 'Venturi tube' equality
meaning 'if the left is defined then so is the right and they are equal'.
We spoke above of the informal convention in mathematics. It seems that many
authors are actually doing something like defining the equality predicate
contextually. This seems surprising when equality is considered such a basic
thing, but the conclusion is hard to avoid when one sees phrases like 'if y
is the unique value with (x,y)  f, we write f(x) = y'. This isn't
specific to a foundational discussion of function application; many analysis
texts do similar things for the limiting operation, for example. In fact it's
rather common to see mathematics books make 'conditional' definitions --- 'if
x is ..., then we define f(x) = E[x]' rather than just 'we define f(x)
= E[x]' --- again, there is probably a wish to have certain contextual
information carried around with the definition. Set theory texts are
occasionally more precise, e.g. they may say 'f(x) is the (unique) y such
that (x,y)
f, we write f(x) = y'. This isn't
specific to a foundational discussion of function application; many analysis
texts do similar things for the limiting operation, for example. In fact it's
rather common to see mathematics books make 'conditional' definitions --- 'if
x is ..., then we define f(x) = E[x]' rather than just 'we define f(x)
= E[x]' --- again, there is probably a wish to have certain contextual
information carried around with the definition. Set theory texts are
occasionally more precise, e.g. they may say 'f(x) is the (unique) y such
that (x,y)  f'. One formalization of this, made explicit by
[rosser-ml], is as a descriptor term
f'. One formalization of this, made explicit by
[rosser-ml], is as a descriptor term  y. (x,y)
y. (x,y)  f, but,
depending on the precise semantics of the descriptor and the logic, this can
mean different things.
f, but,
depending on the precise semantics of the descriptor and the logic, this can
mean different things.
It is important not only that a convention for handling partial functions
should have attractive mathematical features, but also that it should remain
intuitive. Users must be aware, for example, that 0/0 = 0, or that s = t
may hold even if both s and t are undefined. If there are arcane features
hidden inside the logic, these can be damaging to the fancied clarity of formal
mathematics. As [arthan-undefinedness] remarks 'all but the most expert
readers will be ill-served by formal expositions which make use of devious
tricks'. For this reason, we do not find very elaborate schemes for dealing
with partial functions, such as the use of a 3-valued logic, so attractive.
Arthan goes further, claiming that that 'in an ideal world, the subtleties of
different treatments of undefinedness should not be a central concern for
people writing specifications. In our experience, most real-life specifications
that do make essential use of undefined terms are just wrong --- they do not
say what their author intended.' Though this is based on experience of computer
system specification rather than pure mathematics, it may still hold true
there.



 John Harrison
1996/8/13; HTML by
John Harrison
1996/8/13; HTML by  1996/8/16
1996/8/16
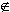 dom(f) as something arbitrary; in effect we are expanding the
domain of f but saying nothing about the values it takes there.
Alternatively, we can specify an explicit value for arguments outside the
domain; this approach can be exploited by choosing a particularly convenient
one. For example, if we decide 0-1 = 0, we have lots of nice unconditional
theorems, like
dom(f) as something arbitrary; in effect we are expanding the
domain of f but saying nothing about the values it takes there.
Alternatively, we can specify an explicit value for arguments outside the
domain; this approach can be exploited by choosing a particularly convenient
one. For example, if we decide 0-1 = 0, we have lots of nice unconditional
theorems, like  x
x  R. (x-1)-1 = x,
R. (x-1)-1 = x,  x
x  R.
-x-1 = (-x)-1,
R.
-x-1 = (-x)-1,  x, y
x, y  R. (x y)-1 = x-1 y-1 and
R. (x y)-1 = x-1 y-1 and
 x
x  R. x-1
R. x-1  0
0  x
x  0. However some may regard these
theorems as pathological, obscene or simply untrue. Actually even if an
arbitrary value is chosen, these freak theorems show up occasionally. If we
define, as one normally would, x / y = x y-1, then 0 / 0 = 0, because
whatever 0-1 might be, it's some real number, and multiplying it by zero
gives zero! In an untyped system this problem happens less (in the example
given we wouldn't even know that 0-1
0. However some may regard these
theorems as pathological, obscene or simply untrue. Actually even if an
arbitrary value is chosen, these freak theorems show up occasionally. If we
define, as one normally would, x / y = x y-1, then 0 / 0 = 0, because
whatever 0-1 might be, it's some real number, and multiplying it by zero
gives zero! In an untyped system this problem happens less (in the example
given we wouldn't even know that 0-1  R), but does not disappear
completely.
R), but does not disappear
completely.


 Y to total
functions X
Y to total
functions X  Y, using the value Y to denote undefinedness.
Y, using the value Y to denote undefinedness.

 n
n  depend on quite small details of how the typechecking and basic logic interact.
depend on quite small details of how the typechecking and basic logic interact.
 y. (x,y)
y. (x,y) 
 John Harrison
1996/8/13; HTML by
John Harrison
1996/8/13; HTML by  1996/8/16
1996/8/16